the wavelength emitted by the source
This means, as emitted by the source if it were in a stationary laboratory.
\(\Delta \lambda=\left(\lambda_{lab}-\lambda_{observed}\right)\)
So \(\frac{\Delta \lambda}{\lambda}\) is the percent change in wavelength.
Similar expressions exist for frequencies \(f_{lab}\) and \(f_{observer}\)
describe changes in the wavelengths of radio waves or X-rays
So a radio wave that has a smaller frequency than normal is redshifted. An xray wave with a higher frequency is blueshifted... all of this even though we do not perceive radio or xray as having color.
Color Shifts
This is the main concept to focus on, for Doppler shifting. Redshift and blueshift are commonly used tools for studying galaxy clusters, galaxies, stars, planets and even atoms.
Volcanoes
There are tons of volcanoes in the solar system. The largest volcano we know of is on Mars!!
This is the way many, but not all, of the mountain ranges on Earth were formed.
Another example: the Himalayas. They formed when the subcontinent of India bashed northward into Eurasia.
astronomy exams
Hmmmm...
It is a cooling system for the planet.
Convection!!
Heat escaping from the interior provides energy for the formation of our planet’s mountains, valleys, volcanoes, and even the continents and ocean basins themselves.
Main source of forces and motion = convection. Huge blobs of molten lava convect from core to surface, like water boiling in a pot on the stove or a thunderstorm convecting water vapor and liquid water in the atmosphere.
white
or pinkish up in Georgia!!!!
To find primitive rock, we must look to smaller objects such as comets, asteroids, and small planetary moons
Yup -- asteroids and comets are chunks of history going all the way back.
Metamorphic rocks
Good example, if you've been camping in Georgia, is the Pine Mountain formation, which includes a lot of quartzite.
I have a chunk of it on my desk in the Physical Sciences Building, something like this:
common sandstones, shales, and limestones
Consider, for example, the layers of sedimentary rocks in the Grand Canyon.
Jupiter’s moon Io
We will have a lot to say about Io.
rework the surface of our planet constantly
Unlike some moons and planets which are geologically dead. Good example of dead geologically is our moon.
radar-bright water ice
This means that water ice has a relatively high radar reflectivity. It does not dissipate the incoming radar beam, but bounces back a lot: strong return signal, "bright."
most important discoveries was the verification of water ice
Astronomers are always looking for signs of water on planets, comets, asteroids, moons and on exoplanets.
resulting Doppler shift
Here is a freight train blowing its horn as it passes the rail fan's video camera. At about 0:39, the horn shifts from a high note (while approaching) to a lower note (while moving away from the camera).
This is a Doppler Shift for sound waves.
Electromagnetic waves -- radar, visible light, even xrays -- also experience Doppler shifting. It is how the sheriff's deputy nabs speeders with his radar gun, and it is how we can measure velocities toward or away from Earth.
radius
Also using a radar rangefinder.
mass
Using Kepler's third law and a radar rangefinder to actually get the orbit.
at least part of the core must be liquid
Also similar to Earth's core. However the metallic part of Earth's core is not nearly as big a fraction of Earth, compared to Mercury
silicates
Sand is a silicate mineral -- most white sands are principally silicon dioxide \(Si\:O_2\).
metallic iron-nickel core
Earth also has iron/nickel core
its orbit has the high eccentricity of 0.206, Mercury’s actual distance from the Sun varies from 46 million kilometers at perihelion to 70 million kilometers at aphelion
Here is a set of diagrams that show the aphelion and perihelion in true proportion,
The Atomic Nucleus
Study this section carefully: Basic info for using isotopes
Probing the Atom
Skim this section for basic information about the discovery of the structure of atoms. Prior to Rutherford, we though atoms were just blobs of something sprinkled with electrons.
The Bohr Atom
Skim this section, because it relates to discrete spectra, one of our important tools in astronomy.
The number of neutrons is not necessarily the same for all atoms of a given element.
Conceptual definition of isotope. It is the number of protons that defines which element you have, but the nucleus can have any amount of neutrons it can hold onto.
The type of element is determined by the number of protons in the nucleus of the atom
IMPORTANT definition!!!!
They are also shown much closer than they would actually be
This is the remarkable fact about atoms: they are mostly empty space! Makes a person think.
Geologists estimate that about half of Earth’s current internal heat budget comes from the decay of radioactive isotopes in its interior.
Which helps keep lava in its molten state!
This graph
Excellent graph and caption, visual definition of half life.
if we have a very large number of radioactive atoms of one type (say, uranium), there is a specific time period, called its half-life, during which the chances are fifty-fifty that decay will occur for any of the nuclei.
A lovely definition of half-life!
emission of particles such as electrons
Like radioactive carbon-14 \(^{14}C\) spontaneously emitting an electron from its nucleus to become nitrogen-14 \(^{14} N\) which is stable. Most nitrogen, 99.632%, is nitrogen-14.
Scientists measure the age of rocks using the properties of natural radioactivity.
Using the idea of "radioactive half-life" of an element.
This composite image of the Moon’s surface
Compared to Earth, where impact craters are rare, the Moon is loaded with craters. That is because Earth has weather, volcanoes, earthquakes and continental drift.
snow
For Florida students, this term, snow, indicates a rare solid form of \(H_2 O\) which,at low temperatures, forms six-sided crystals that are very cold and fall from the upper atmosphere. Rare in Florida since the last Ice Age.
potential solutions to most of the major problems raised by the chemistry of the Moon
Important parts of the theory, though it is not yet a stone cold lock.
a “bullet” about the size of Mars
nicknamed Theia
increasing evidence
Cf., mentions of oxygen isotopes in Lecture 8 Spring '18, (Edward D. Young et al. Science 2016;351:493-496) especially the relation of lunar materials to terrestrial rocks like the Mauna Loa lavas.
major isotopes1 of oxygen,
Cf., lecture 8, Spring '18
nearly circular orbit our Moon occupies today.
$$e=0.055$$
Cf., the NASA Space Science Data Center planetary fact sheet.
Moon is both tantalizingly similar to Earth and frustratingly different.
Yes, as the moon rocks from Apollo show. They have been analyzed for decades and compared to terrestrial rocks.
whip through the inner parts of their orbits
...where they are also heated up by the sun and become visible.
According to Kepler’s second law, therefore, they spend most of their time far from the Sun, moving very slowly
Important concept. They loiter out by their aphelion, but when they get in close to perihelion, they are really moving fast. So visible comets are only visible for weeks, if that.
Both asteroids and comets are believed to be small chunks of material left over from the formation process of the solar system.
Unlike the surface rocks most places on Earth. E.g., the Florida limestone bedrock which, in its oldest layers, is about 35 million years, less than 1% of the age of the solar system.
Otherwise the pre-telescopic observations of Brahe would not have been sufficient for Kepler to deduce that its orbit had the shape of an ellipse rather than a circle.
This is the part that always astounds me, that Kepler spotted this small amount of eccentricity!
5 kilometers per second
"only" 11,000 mph!
48 kilometers per second
about 107,000 mph!!
The average orbital data for the planets
I usually use NASA's Planetary Fact Sheet. All sorts of neat data.
perigee and apogee
Similar to aphelion and perihelion but relative to Earth. You hear the guys at Mission Control in Houston talk about perigee and apogee. E.g., the ISS right now has perigee of 408 km altitude, apogee of 410 km altitude.
Two points in any orbit in our solar system have been given special names.
Important vocabulary terms: aphelion and perihelion.
Halley
Not labeled well, but compare to the Mini-Lecture A in YouTube.
The Discovery of Neptune
We will discuss this after Exam 1.
parabola, and hyperbola
There are objects that pass through the solar system on parabolic and hyperbolic orbits,
such as the mysterious A/2017 U1 'Oumuamua (YouTube of its trajectory)
beyond the orbit of Pluto.
Pluto the dwarf planet has a semimajor axis about 39.482 AU. Its orbital period is about 248 years
Kepler’s third law
A huge topic for us this entire semester.
Note that the eccentricities of the planets’ orbits in our solar system are substantially less than shown here.
Correct. Comets and asteroids, however, do commonly have ellipticity of this level or more.
The universe could be a bit more complex than the Greek philosophers had wanted it to be.
The scientific end of the celestial spheres, although celestial sphere is still a lovely image outside of science. : )
Kepler found that Mars has an elliptical orbit, with the Sun at one focus (the other focus is empty). The eccentricity of the orbit of Mars is only about 0.1; its orbit, drawn to scale, would be practically indistinguishable from a circle, but the difference turned out to be critical for understanding planetary motions.
Because even Mars is so close to a perfect circle, it has always amazed me that Kepler spotted it.
If the foci (or tacks) are moved to the same location, then the distance between the foci would be zero. This means that the eccentricity is zero and the ellipse is just a circle; thus, a circle can be called an ellipse of zero eccentricity. In a circle, the semimajor axis would be the radius.
Good to keep in mind: a circle is just a specially symmetric case of an ellipse, \(e=0\)
The ratio of the distance between the foci to the length of the major axis is called the eccentricity of the ellipse.
$$e=\sqrt{1-\frac{b^2}{a^2}}$$
We wrap the ends of a loop of string
Cf.,"pin and string method" on YouTube.<br />
sum of the distance from two special points inside the ellipse to any point on the ellipse is always the same
Technical definition of ellipse, sounds rough... HOWEVER, it is the reason that the string method in Fig. 3 works. The length of the string is "always the same," if you are careful.
observations
Observations can be refined but not ignored or contradicted!
behavior of planets based on their paths through space.
"...based on their paths." This is bass ackward relative to, e.g., Ptolemy. For Ptolemy, he based everything on circles and forced everything into a complex system involving epicycles, deferents, equants etc. To some degree, Copernicus and Galileo were also stuck thinking "circles." Kepler, however, took the path that Nature showed him in Tycho's measurements -- especially Mars' ellipse -- and then figured out a pattern from that. And he figured out three patterns, actually.
occupied most of Kepler’s time for more than 20 years
What a career-length project!
Tubingen
Still a great university in Germany!!
Brahe didn’t have the ability to analyze them
...but Kepler did!!!
exploding star
A supernova, 1572. Cf., APOD 03/17/09
Three years after the publication of Copernicus’ De Revolutionibus, Tycho Brahe was born
This shows the slowness of scientific development in those days.
The square of a planet’s orbital period is directly proportional to the cube of the semimajor axis of its orbit.
We now leverage Kepler's Third Law to use in any star system for which we can measure orbital distance, e.g., by parallax, and orbital periods. Black holes, which we cannot see, can reveal themselves in this way.
Learning Objectives
Focus on the subsection "Orbital Motion and Mass."
Calculating the Effects of Gravity
Bypass this calculation until end of the semester.
Including the mass term allows us to use this formula in a new way. If we can measure the motions (distances and orbital periods) of objects acting under their mutual gravity, then the formula will permit us to deduce their masses.
Here is the crucial strategy for astronomers!
There are many situations in astronomy, however, in which we do need to include the two mass terms
This means that the sum of the Sun’s mass and a planet’s mass, (M1 + M2), is very, very close to 1.
Here are the two masses:
So in terms of \(M_{\odot}\), the terms \(M_1 + M_2=1.0000030035\) which is really close to 1.
By the end of this section
Skim this section except carefully read the paragraphs about
When a spinning figure skater
Important for the entire semester, because angular momentum of galaxies, supernova detonations and black holes are important.
on a well-oiled swivel stool by starting yourself spinning slowly with your arms extended and then pulling your arms in.
We have 8 videos in YouTube from lecture hall demonstrations on a lab stool, as described. Have a look.
Kepler’s second law is a consequence of the conservation of angular momentum.
I.e., Kepler's equal areas law is a consequence of the same principle you observe while watching ice skaters at the Olympics: they spin WAY faster when they bring their arms in, but their spin slows down when they bring their arms in.
Mass, Volume, and Density
Skip this for now
This is the principle behind jet engines and rockets
...as I mentioned above!
This means that forces in nature do not occur alone
Good description. This is one way to say that gravitation is universal.
mass times its velocity
Momentum p, $$p=mv$$
For every action there is an equal and opposite reaction
Newton's third law is
In the original Latin, the three laws contain only 59 words
59 words that changed the world!
Philosophiae Naturalis Principia Mathematica.
Extremely influential even in this our day.
his friend Edmund Halley
What a fruitful friendship!
born in Lincolnshire, England, in the year after Galileo’s death
Another indication of the slowness of scientific development in that era.
This animation (http://tiny.cc/88cyqy) shows the phases of Venus. You can also see its distance from Earth as it orbits the Sun. The Astronomy Picture of the Day has an animation of Venus https://apod.nasa.gov/apod/ap060110.html (http://tiny.cc/vadyqy) and a set of images of Venus as viewed from Earth. https://apod.nasa.gov/apod/ap170317.html (http://tiny.cc/ebdyqy)
Cool animations!
in those days, before the telescope, no one imagined testing these predictions.
Galileo observed the phases of Venus in the century after Copernicus.
predictions
YES! This is what scientists want to do: predict the position of a previously unseen planet like Neptune, predict the landing place of a spacecraft sent to Mars, etc.
still taught at Harvard University
but not at UCF, of course!! ;)
simple experiment dropping two balls of different weights
I.e., Galileo's famous experiment at the leaning tower of Pisa!
philosophical tradition, going back to the Greeks and defended by the Catholic Church, held that pure human thought combined with divine revelation represented the path to truth
Galileo broke out of this tradition by his emphasis on
clumsy and lacking the beauty and symmetry of its successor.
Symmetry is a powerful tool, because it is not subjective -- it can be expressed mathematically. E.g., the symmetry of positive and negative numbers relative to zero, whereby \(\left( -2 \right)^2 = \left( 2\right)^2\) and both \(=4\)
the nearer a planet is to the Sun, the greater its orbital speed.
Sir Isaac Newton figured out why this is true, in his theory of universal gravitation -- which is a few chapters ahead.
We have all experienced seeing an adjacent train, bus, or ship appear to move, only to discover that it is we who are moving.
This is called Galilean relativity. Galileo studied relative motion. Einstein's relativity was a refinement on Galileo, but with enormous implications like black holes.
heavenly bodies must be made up of combinations of uniform circular motions.
It was left to Johannes Kepler to break this concept.
His great contribution to science was a critical reappraisal of the existing theories of planetary motion and the development of a new Sun-centered, or heliocentric, model of the solar system.
Good description, in a nutshell, for Copernicus' contribution
We can now take a brief introductory tour
Don't forget to review the "syllabus" type YouTube, https://youtu.be/7jSqOscLwWs
In this simplified model of a hydrogen atom
A very important diagram to keep in mind for most topics this semester, because most of the information about the stars and galaxies of the universe comes to us from starlight and its spectral lines!
We can use Kepler’s law (see Orbits and Gravity) and our knowledge of the visible star to measure the mass of the invisible member of the pair.
One short sentence, but powerful. Thank you, Professor Kepler!
they are actually valid for all bodies satisfying the two previously stated conditions.
A short sentence, but powerful.
Laminar flow is characterized by the smooth flow of the fluid in layers that do not mix. Turbulent flow, or turbulence, is characterized by eddies and swirls that mix layers of fluid together.
Good comparison of idealized laminar flow with turbulent flow. Planes spew wake turbulence, very dangerous for following aircraft.
If we follow a small volume of fluid along its path,
Typical strategy for understanding fluid dynamics.
This equation tells us that, in static fluids, pressure increases with depth
We already knew this.
pressure has units of energy per unit volume, too.
Interesting to think of pressure prepresenting energy independent of bulk motion or position of the center of mass of a pixel of fluid.
Bernoulli’s equation is a form of the conservation of energy principle.
Good concept to remember.
The net work done increases the fluid’s kinetic energy. As a result, the pressure will drop in a rapidly-moving fluid, whether or not the fluid is confined to a tube.
Informal way of stating the Bernoulli principle.
When a fluid flows into a narrower channel, its speed increases.
Sound in solids can be both longitudinal and transverse.
E.g., the s and p waves from earthquakes, although the liquid outer core of Earth does not permit s waves to propagate, because s waves are transverse.
In equation form
Generic wave equation. For electromagnetic radiation, the wave equation is \(c=\lambda f\), where the speed of light \(c=3\times 10^8 \frac{m}{s}\).
and energy
Also momentum. Because electromagnetic radiation propagates momentum and energy across spacetime, we have an opportunity to harness sunlight in outer space and use it in a solar sail, to navigate here and there in the solar system.
For earthquakes, there are several types of disturbances, including disturbance of Earth’s surface and pressure disturbances under the surface.
Another seismic wave phenomenon is a seiche
Cf., What is a seiche?
The displacement as a function of time t in any simple harmonic motion
We discussed this in Lecture 32
PERIOD OF SIMPLE HARMONIC OSCILLATOR
We worked on this in Lecture 33.
most fishermen feel no obligation to truthfully report the mass
Good one. 
potential energy stored in a spring
Huge concept. It applies from the Big Bang Theory origin of the universe down to the quantum world of electrons and photons and nuclei.
elastic potential energy
I usually call is SPE, spring potential energy, to distinguish from EPE, electrostatic potential energy. But I will try to use EPE in our lectures! : )
solve
It is interesting to look up various spring constants for springs one can purchase. E.g., this website for Century Springs shows the spring constant as a "rate," in pounds per inch instead of N/m.
Here, is the restoring force, is the displacement from equilibrium or deformation, and is a constant related to the difficulty in deforming the system. The minus sign indicates the restoring force is in the direction opposite to the displacement.
See previous note.
The simplest oscillations occur when the restoring force is directly proportional to displacement.
Concise definition:
Good.
dissipative forces
e.g., friction, aerodynamic drag etc.
superposition and interference
Critical for understanding the periodic table, electronegativity, covalent bonding and may more topics in PHY2054 and beyond.
Many systems oscillate, and they have certain characteristics in common.
True. And this is why physicists spend so much time thinking about spring/mass systems.<br>
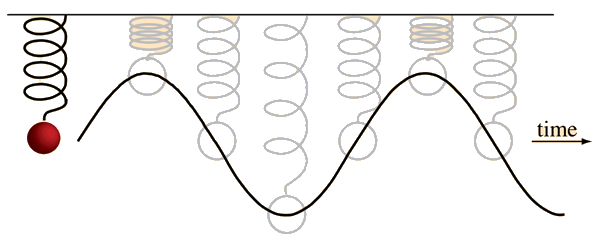That is, what is simple to learn about spring/mass systems becomes widely applicable in other oscillatory systems like a beating heart, a particle inside an atom's nucleus, a light wave, a tsunami etc.
beating of hearts
IMPORTANT.
Electrocardiologists make a "phase space reconstruction" (PSR) of a patient's electrocardiogram, 
knowing that a regular sinus rhythm is a very specific oscillatory system, whereas fibrillation, tachycardia etc. are NOT oscillatory. Cf., G.Koulaouzidis, S. Das et al. "Prompt and accurate diagnosis of ventricular arrhythmias with a novel index based on phase space reconstruction of ECG" International Journal of Cardiology, 2015-03-01, Volume 182, Pages 38-43. DOI: 10.1016/j.ijcard.2014.12.067
guitar, atoms
Atoms and guitars ← ← you will savvy this analogy in PHY2054C!!
four types of waves in this picture
Wonderful!
10.4
Ready to work on this topic starting 03/27
Rotational Kinetic Energy
Very cool topic to complete the rotational analogies, but I will reserve this for after Exam 3.
Three children are riding on the edge of a merry-go-round that is 100 kg, has a 1.60-m radius, and is spinning at 20.0 rpm. The children have masses of 22.0, 28.0, and 33.0 kg. If the child who has a mass of 28.0 kg moves to the center of the merry-go-round, what is the new angular velocity in rpm?
Brain burner calculation. I will do a talking PDF for this one.
Compare this angular momentum with the angular momentum of Earth on its axis.
Spin angular momentum calculation, using the table of moments of inertia.
Calculate the angular momentum of the Earth in its orbit around the Sun.
Planetary angular momentum calculation
Conceptual Questions
Notice how many conceptual questions there are? That is significant.
Suppose a child walks from the outer edge of a rotating merry-go round to the inside. Does the angular veloc
Good conceptual question
Calculating the Angular Momentum
It is enough for us to predict "larger \(\omega\)" or "smaller \(\omega\)" etc., and not necessarily calculate L to the nearest \(0.001 \,kg\,m^2\). After Exam 3, we will do some full calculations, however.
In the next image, her rate of spin increases greatly when she pulls in her arms, decreasing her moment of inertia.
As a student observed, \(I\) and \(\omega\) vary inversely when angular momentum is conserved.
These expressions are the law of conservation of angular momentum. Conservation laws are as scarce as they are important.
Our demonstrations with the hand weights and rotating lab stool on Friday were to demonstrate conservation of angular momentum, a huge concept from astrophysics all the way down to quantum mechanics.
The equation is very fundamental and broadly applicable.
target for lecture, 03/22/19
Starting with the formula for the moment of inertia of a rod rotated around an axis through one end perpendicular to its length prove that the moment of inertia of a rod rotated about an axis through its center perpendicular to its length is You will find the graphics in Figure 3 useful in visualizing these rotations.
This would be easy to figure out as a lecture exercise, but not on Exam 3.
Calculate the moment of inertia of a skater given the following information. (a) The 60.0-kg skater is approximated as a cylinder that has a 0.110-m radius. (b) The skater with arms extended is approximately a cylinder that is 52.5 kg, has a 0.110-m radius, and has two 0.900-m-long arms which are 3.75 kg each and extend straight out from the cylinder like rods rotated about their ends.
This would not be a brain burner, to make you think, but a rotational torture device. I will not put ANYTHING like this on Exam 3.
Why is the moment of inertia of a hoop that has a mass and a radius greater than the moment of inertia of a disk that has the same mass and radius?
We actually discussed the answer to this question in Friday lecture.
MAKING CONNECTIONS
Extensive discussion about this Figure 3 in Friday's lecture.
torque is analogous to force, angular acceleration is analogous to translational acceleration, and is analogous to mass (or inertia). The quantity is called the rotational inertia or moment of inertia of a point mass a distance from the center of rotation.
Big topic during most recent lectures
Example 1: Calculating the Effect of Mass Distribution on a Merry-Go-Round
We will be demonstrating this stuff in lecture, 03/22/19
Some rotational inertias.
All of these moments of inertia are the result of counting up the quantity \(mr^2\) for each pixel of mass, \(I=\sum_{\text{pixels}} \left(mr^2\right)\) To do this task, you usually need calculus, although the hoop can be done with straight trig, no calc.
Notice that each moment of inertia is a fraction or multiple of total mass \(M\) multiplied by the square or sum of squares of the overall dimension \(R^2\) or \(a^2+b^2\) etc. That is because each object in the table has some symmetry which simplifies the calculus and therefore simplifies the formula.
Kinematics of Rotational Motion
Not a total bypass but we did not talk too much about this information in lecture.
At its peak, a tornado is 60.0 m in diameter and carries 500 km/h winds. What is its angular velocity in revolutions per second?
Basic calculation of \(\omega\)
Explain why centripetal acceleration changes the direction of velocity in circular motion but not its magnitude. 3: In circular motion, a tangential acceleration can change the magnitude of the velocity but not its direction. Explain your answer.
I discussed these two questions at length in lecture
Analogies exist between rotational and translational physical quantities. Identify the rotational term analogous to each of the following: acceleration, force, mass, work, translational kinetic energy, linear momentum, impulse.
Would make a good matching set. : )
Centripetal acceleration ac occurs as the direction of velocity changes; it is perpendicular to the circular motion. Centripetal and tangential acceleration are thus perpendicular to each other.
We discussed this in lecture.
Forces and Torques in Muscles and Joints
Bypass until you are ready to take MCAT or are already in med school, PT school etc.
Simple Machines
Bypass, although it is an interesting section to read if you are interested.
Applications
Bypass
Two children of mass 20.0 kg and 30.0 kg sit balanced on a seesaw with the pivot point located at the center of the seesaw. If the children are separated by a distance of 3.00 m, at what distance from the pivot point is the small child sitting in order to maintain the balance?
Basic calculation
chickens
Forget about the chicken
Two children push on opposite sides of a door during play.
Good calculation of medium difficulty.
When opening a door, you push on it perpendicularly with a force of 55.0 N at a distance of 0.850m from the hinges. What torque are you exerting relative to the hinges?
Basic calculation
Introduction to Rocket Propulsion
We have talked about rocket motors and their effects, but consider this section is a bypass.
It can be shown that
Biggest lie in physics. "It can be shown that..." is usually the place where the author is thinking about calculus but does not want to actually show it.
Collisions of Point Masses in Two Dimensions
Bypass until after Exam 3
Inelastic Collisions in One Dimension
Bypass
A bullet is accelerated down the barrel of a gun by hot gases produced in the combustion of gun powder. What is the average force exerted on a 0.0300-kg bullet to accelerate it to a speed of 600 m/s in a time of 2.00 ms (milliseconds)?
Basic impulse calculation
A runaway train car that has a mass of 15,000 kg travels at a speed of down a track. Compute the time required for a force of 1500 N to bring the car to rest
Classic stopping time problem. Use the impulse equation, though: \(F_{net} \Delta t = \Delta p\)
What is the mass of a large ship that has a momentum of when the ship is moving at a speed of (b) Compare the ship’s momentum to the momentum of a 1100-kg artillery shell fired at a speed of 3
Battleship recoil problem. I like it.
Calculate the momentum of a 2000-kg elephant charging a hunter at a speed of (b) Compare the elephant’s momentum with the momentum of a 0.0400-kg tranquilizer dart fired at a speed of (c) What is the momentum of the 90.0-kg hunter running at after missing the elephant?
Basic momentum calculations.
An object that has a small mass and an object that has a large mass have the same momentum. Which object has the largest kinetic energy? 2: An object that has a small mass and an object that has a large mass have the same kinetic energy. Which mass has the largest momentum?
Two good study questions.
Example 2: Calculating Force: Venus Williams’ Racquet
Good.
World Energy Use
Bypass
Work, Energy, and Power in Humans
Bypass
Power
Bypass for now.
Conservation of Energy
Bypass, although it is interesting. Our main concern, the conservation of total mechanical energy, \(E=GPE+KE\) was developed in a previous section of Ch. 7
Nonconservative Forces
Bypass
Potential Energy of a Spring
Bypass until after Exam 3.
This equation means that the total kinetic and potential energy is constant for any process involving only conservative forces.
Conservation of total mechanical energy $$E = GPE+KE$$ which we used on Written HW 07.
A 100-g toy car is propelled
A good brain burner. I will try to do a talking PDF of this one.
Suppose a 350-g kookaburra
Good basic problem.
9-megaton fusion bomb
ridiculous
What is the final speed of the roller coaster
Very similar to Written HW 07 calculation of escape velocity
this point is arbitrary;
Correct. You can set the zero of any potential energy wherever you like, as long as you stay consistent all the way through your calculations. The reason for this is that work is done when there is a \(\Delta \left(GPE \right)\)
Because gravitational potential energy depends on relative position, we need a reference level at which to set the potential energy equal to 0.
Note: in the geospatial mini-lecture, the zero of GPE was at infinity.
An object’s gravitational potential is due to its position relative to the surroundings within the Earth-object system.
The reason for this is that GPE exists because of an interaction of two bodies: Earth and the other object under consideration
we refer to this as the
Dr. Brueckner refers to it as GPE
A car’s bumper is designed to withstand a 4.0-km/h (1.1-m/s) collision with an immovable object without damage to the body of the car. The bumper cushions the shock by absorbing the force over a distance. Calculate the magnitude of the average force on a bumper that collapses 0.200 m while bringing a 900-kg car to rest from an initial speed of 1.1 m/s.
A good brain burner. I will make this one into a talking PDF.
How fast must a 3000-kg elephant move to have the same kinetic energy as a 65.0-kg sprinter running at 10.0 m/s?
Another good basic comparison of KE.
Compare the kinetic energy of a 20,000-kg truck moving at 110 km/h with that of an 80.0-kg astronaut in orbit moving at 27,500 km/h.
Basic comparison. Good.
lawn mower.
I detest the lawn mower example. YUKKKK
On the whole, solutions involving energy are generally shorter and easier than those using kinematics and dynamics alone.
This is why scientists work most of quantum mechanics and relativity in terms of energies, not F = ma forces.
Example 4: Work and Energy Can Reveal Distance, Too
Stopping distance problem, a classic exercise
rotational kinetic energy
Rotational KE is simple to handle, but we will tackle it after Exam 3.
This expression
Work and change in kinetic energy, \(W=\Delta \left( KE \right)\)
Figure 1. (a) A graph
Discussed this in lecture.
How much work is done by the boy pulling his sister 30.0 m in a wagon as shown in Figure 3? Assume no friction acts on the wagon
A good basic work calculation in two dimensions.
2: A 75.0-kg person climbs stairs, gaining 2.50 meters in height. Find the work done to accomplish this task.
Reminiscent of the concepts in Written HW 07
2: Give an example of a situation in which there is a force and a displacement, but the force does no work. Explain why it does no work.
Good question. Under what conditions will an applied force do zero work? It is a geometric question, really.
work done on a system by a constant force is defined to be the product of the component of the force in the direction of motion times the distance through which the force acts.
$$F_{||} \Delta s$$
2: Calculate the mass of the Sun based on data for Earth’s orbit and compare the value obtained with the Sun’s actual mass.
Good mini-workout
a small set of rules and a single underlying force
This is why Halley's successful prediction was so important.