This equation seems logical enough.
Actually has to do with the idea of flux, which we will also use in electromagnetism, e.g., a magnetic field flux, Fig. 4, Ch. 23.1
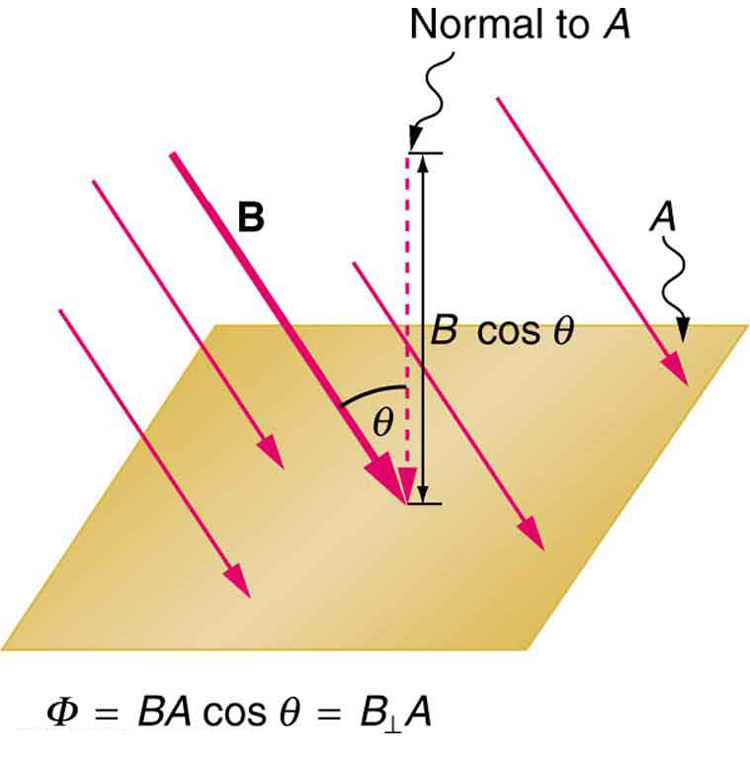
This equation seems logical enough.
Actually has to do with the idea of flux, which we will also use in electromagnetism, e.g., a magnetic field flux, Fig. 4, Ch. 23.1

volume of water contained in a 6-lane 50-m lap pool
Amazing
volume of fluid passing by some location through an area during a period of time
so units of volume/second
If its average density is less than that of the surrounding fluid, it will float.
Like a fireball rising through much cooler air.
 "Fire Breather" by Jon_Senior is licensed with CC BY-NC-ND 2.0. To view a copy of this license, visit https://creativecommons.org/licenses/by-nc-nd/2.0/
"Fire Breather" by Jon_Senior is licensed with CC BY-NC-ND 2.0. To view a copy of this license, visit https://creativecommons.org/licenses/by-nc-nd/2.0/
Example 1: Calculating Height of IV Bag: Blood Pressure and Intravenous Infusions
Nice.
Mercury manometers are often used to measure arterial blood pressure.
...in the doctor's office
Gauge pressure is positive for pressures above atmospheric pressure
E.g., at Wawa, an extra 32 PSI above the ambient air pressure.

atmospheric pressure has no net effect on blood flow
This is why "they" say that you should keep the blood pressure sleeve at approximately the level of your heart.
 "Blood pressure check" by Army Medicine is licensed with CC BY 2.0. To view a copy of this license, visit https://creativecommons.org/licenses/by/2.0/
"Blood pressure check" by Army Medicine is licensed with CC BY 2.0. To view a copy of this license, visit https://creativecommons.org/licenses/by/2.0/
2: What force must be exerted
Good workout for a study problem.
MAKING CONNECTIONS: CONSERVATION OF ENERGY
We will work out this idea in lecture.
This value
Good force multiplier
providing the pistons are at the same vertical height
so that there is no pressure differential due to \(\Delta z\) elevation difference, i.e., \(\rho g\Delta z\)
those that operate car brakes
Brake fluid is not water. It is usually some kind of glycol ether, very high boiling point and other properties.
Blaise Pascal
Yes, Pascal was a very interesting man, and for more reasons than are mentioned here.
pressure so important in fluids
This is what makes a hydraulic system so useful for tranmitting and exerting huge forces, like excavation machines.

Discussion
Sometimes you see depth for scuba divers rated in atmospheres instead of meters. 1.00 atmosphere of depth = 10.3 meters
equivalent to 1 atm),
1013.25 millibars
the thickness of the dam increases with depth to balance the increasing force due to the increasing pressure
...because the designers know how to use calculus, not rough averages
average
Very rough average, but acceptable
the equation
Or, more generally, \(p=\rho g z\) with \(z\) being the vertical coordinate over one’s head toward the zenith
PHET EXPLORATIONS: GAS PROPERTIES
Excellent simulations. I highly recommend them. It is especially nifty to view the diffusion simulation, with data enabled, and watch both sides of the container converge to an equilibrium temperature.
Note that the forces are larger underneath, due to greater depth, giving a net upward or buoyant force that is balanced by the weight of the swimmer.
Important: buoyancy forces.
Example 1: Calculating Force Exerted by the Air: What Force Does a Pressure Exert?
Good example.
In contrast, the same force applied to an area the size of the sharp end of a needle
A friend of mine in the Air Force did a lot of loading of tanks into the big C5-A Galaxy cargo plane. He said that, to save weight, the floor of the cargo bay was not that stout, but that a tank, with its huge weight spread over the big wide treads, would not damage the floor, and a woman walking in high heel shoes would puncture the floor!


weather
E.g., in relation to hurricanes. On the Weather Channel etc., the intensity of a hurricane or tropical storm is usually described by a single number, its central pressure. Hurricane Dorian in 2019 had a central pressure of 910 millibars at its most intense on Sept. 1, 2019 over the Bahamas. Normal atmospheric pressure at sea level on a fair day is higher, 1013.25 millibars. Notice how small a pressure variation that is,
$$\frac{\Delta p}{1013.25\, mb}=\frac{103.25\, mb}{1013.25\, mb}=0.102$$
i.e., about 10%.

Substituting and into the expression for mass gives
This is a lot of mass. \(1.000\text{ metric ton }=1000\, kg\), so this reservoir mass is \(2\times 10^9\, \text{tons}\), two billion metric tone. This is a lot of mass.
TAKE-HOME EXPERIMENT: SUGAR AND SALT
I like this experiment.
Carbon dioxide
Heavier than air
0.917
Why icebergs float!
The metric system was originally devised so that water would have a density of
I always remember this, 1 gram per cubic centimeter.
whether an object sinks or floats in a fluid
Like air bubbles underwater, rising to the surface and expanding as they go.

when the atoms collide
a very small \(\Delta t\) interaction time.
the forces between its atoms
← between the water molecules are hydrogen bonds which you can read about in any standard chemistry textbook/UNIT_3%3A_THE_STATES_OF_MATTER/10%3A_Solids_Liquids_and_Phase_Transitions/10.3%3A_Intermolecular_Forces_in_Liquids).
This rock
This rock looks like a steak...

or maybe a slice of a tree with visible tree rings.

But, okay, we will go with "this rock".
essentially in contact
NOT. They are interacting and the interaction is stable against small spatial perturbations. I.e., it will oscillate around its equilibrium and rapidly radiate off the excess energy to settle back down to the equilibrium distance.
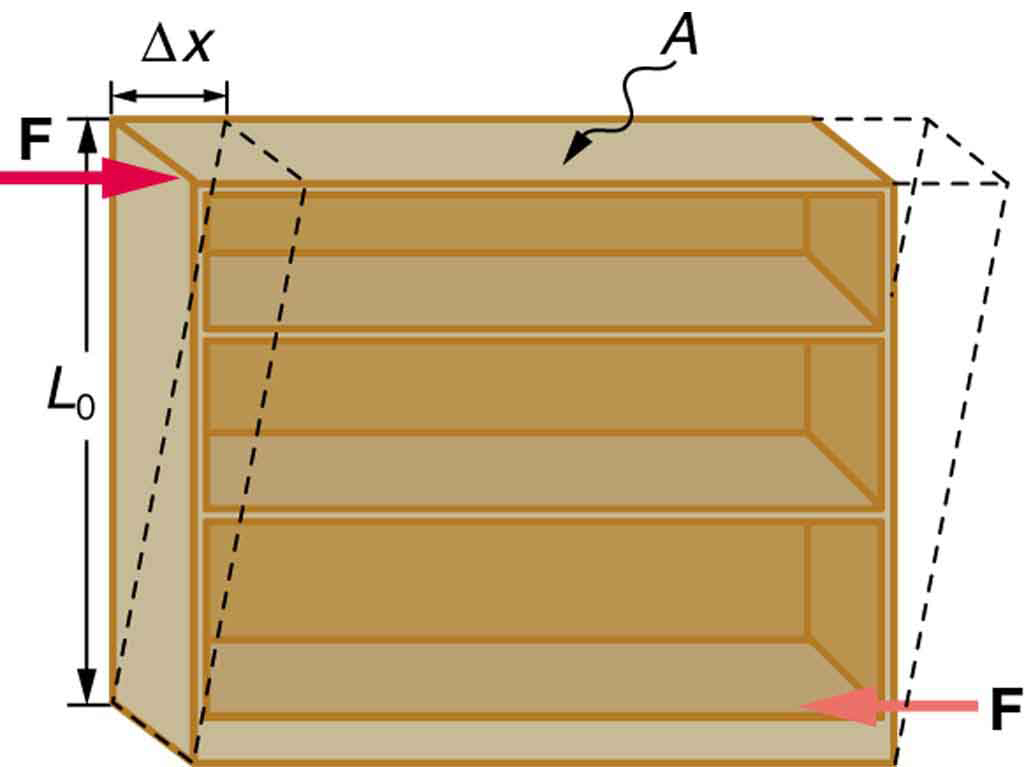
shearing forces
You can read about shearing forces in Chapter 5.3.
It can be shown that
I.e., it can be shown using calculus and a ton of trig!
when scientists began to discover that they are different manifestations of the same force
Hans Christian Ørsted in Denmark, and Michael Faraday in England made this discovery.

electromagnetic forces would completely overwhelm the gravitational force
And, in fact, the electromagnetic forces produced by the muscle fibers in your quadriceps muscles DO overwhelm the gravitational force of the Earth, every time you go up a stairway!

time actually slows down
Time does NOT slow down. However, time measurements by two different observers disagree if the two observers are timing the same events from different positions relative to the "very massive" body, like a black hole.
gravitational force
ALL forms of energy affect the curvature of spacetime
Our weight is the gravitational force due to the entire Earth acting on us.
It is interesting to think about other large, nearby objects that pull gravitationally on us.
$$\text{You }\approx50 - 100\,kg \\ \updownarrow \\ \text{Earth }\approx 6\times 10^24\, kg,\, \\ @ r=6.371\times 10^6 \,m$$
vs.
$$\text{You on the sidewalk @ 350 Fifth Ave., NYC } \\ \approx 50 - 100\,kg\\ \updownarrow \\ \text{Empire State Building }\approx 3.31\times 10^8\, kg,\\ \text{w/ center of mass, elevation } h\approx 200\,m$$
How do those forces compare?
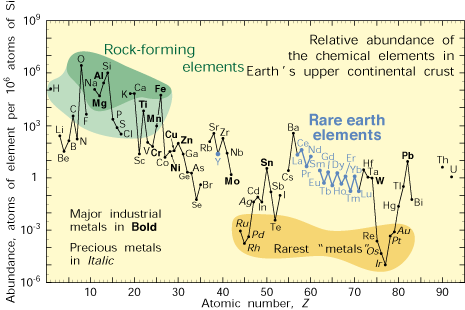
relative abundance of elements in nature
Action at a distance
This topic, action at a distance, has been a topic of scientific discussion for centuries.
microscopic
Should be submicroscopic. VERY submicroscopic!
In fact, nearly all of the forces we experience directly are due to only one basic force
I.e., chemistry! The periods and groups of the periodic table are helpful because they encode the behavior of ELECTRONS in neutral atoms of each element.
 Hinrich's spiral "Programme of Atomechanics"
Hinrich's spiral "Programme of Atomechanics"
at any single point
Instead of an average velocity relative to two points:
where the average speed is
$$\vec{\bar{v}}=\left(\frac{x_2-x_1}{t_2-t_1}\right)\hat{i}+\left(\frac{y_2-y_1}{t_2-t_1}\right)\hat{j}$$
When you take the instantaneous limit, \(\Delta t\longrightarrow 0\) , the other two Δs decrease, also, but the ratios \(\frac{\Delta x}{\Delta t}\) and \(\frac{\Delta y}{\Delta t}\) do not vanish; they converge to a finite value, the components \(v_x\) and \(v_y\)of the instantaneous velocity at time t, where \(t_1<t<t_2\),</p>
$$\vec{v}\left(t\right)=v_x \left(t\right)\hat{i}+v_y \left(t\right)\hat{j}$$
Compare to the \(v\left(t\right)\) formula with the instantaneous limit in the next paragraph.
How fast an object is moving is given by the rate at which the position changes with time.
Two different parameterizations of the path \(\Gamma\), one by increments of (approximately) equal distance, \(t\), and a second parameterization, \(\color{red}\theta\) , as it might be for an aggressive race car driver, with equal increments of time.

For each position xixi{x}_{\text{i}}, we assign a particular time titi{t}_{\text{i}}.
I.e., we parametrize the path along the x-axis.
state where the object is (its position) during its motion
We call this a path parameter. Cf., Parametrizations of Plane Curves in LibreText, for further reading.
other units of length
Like a light-second
$$1.00\, LS= 3.00\times 10^8\, m$$
or the Earth-Sun distance, which we call the astronomical unit,
$$1.00\, AU = 499\, LS$$
etc.
ΔxΔx\Delta x means change in position (final position less initial position)
For any \(\Delta\) the order of subtraction is always
$$\text{final}-\text{initial}$$
$$\text{later}-\text{earlier}$$
and if some kind of sequence exists, \(\left(u_1, u_2, u_3 \ldots\right) \) $$\Delta u=un - u{n-1}$$
We use the uppercase Greek letter delta (Δ) to mean “change in”
Basic vocabulary
Since displacement indicates direction, it is a vector and can be either positive or negative, depending on the choice of positive direction.
Tricky but important point.
we use reference frames that are not stationary but are in motion relative to Earth
...in motion relative to Earth or to any other object. For instance, when docking your capsule to a spacecraft on orbit, you are moving and your target, the spacecraft, is a moving target.

So your sense of steering includes a moving frame of reference. In fact, you are in a frame of reference that is in free fall!
frame of reference
In the usual sense, we can imagine three mutually perpendicular rigid meter sticks...

"starr-160503-4526-Triticum_aestivum-Glenn_seedheads_and_meter_stick_for_height-Hawea_Pl_Olinda-Maui" by Starr Environmental is licensed with CC BY 2.0. To view a copy of this license, visit https://creativecommons.org/licenses/by/2.0/
...but it could be a set of rigid curves, like on this sundial.

"Israel-05367 - Sundial" by archer10 (Dennis) is licensed with CC BY-SA 2.0. To view a copy of this license, visit https://creativecommons.org/licenses/by-sa/2.0/
When you’re in motion, the basic questions to ask are: Where are you? Where are you going? How fast are you getting there?
This is a set of basic questions that apply to a LOT of the scientific enterprise.
if we remove the wall in the middle quickly, the gas expands and fills up the entire container immediately
Joule experiment, free expansion.
The ring travels
A little bit like a wavelet, in that the ring is the source of the reflected wave, on the right hand end of the string.
How the wave is reflected at the boundary of the medium depends on the boundary conditions
Boundary conditions, so important!! Just like initial conditions being important.
16.4 Energy and Power of a Wave
Bypass this chapter section. It is better for a more advanced class, but you may enjoy working through it.
A laser beam
Photons: $$\vec{p}=\hbar\, \vec{k}$$ $$E=\hbar\, \omega$$
16.3 Wave Speed on a Stretched String
Bypass this chapter section. It is better for a more advanced class, but you may enjoy working through it.
That shape is determined by the total energy and angular momentum of the system, with the center of mass of the system located at the focus.
SHAPES OF ORBITS determined by energy and angular momentum states:
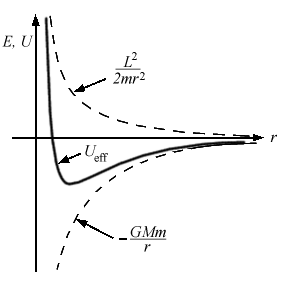
Gravity Away from the Surface
You will use this technology, Gauss' Law, many times in PHY2049
A three-dimensional representation of the gravitational field
the field concept is an abstraction useful here and in PHY2049
an ice skater executing a spin
The Ice Skater Effect. Classic example of conservation of angular momentum.
Conservation of Angular Momentum of a Collision
This example is not even a trick shot in a circus -- i.e., why would anybody want to do this. But it is still illustrative
Dismount from a High Bar
An interesting exercise. The gymnast slows down his spin just in time to land extended to his full height. Requires a lot of practice, probably.
The solar system coalesced from a cloud of gas and dust that was originally rotating.
We discussed this in Session 25
with r being the distance from the point particle to the axis of rotation.
This is an important distinction to make for each and every moment of inertia calculation. The rotation axis
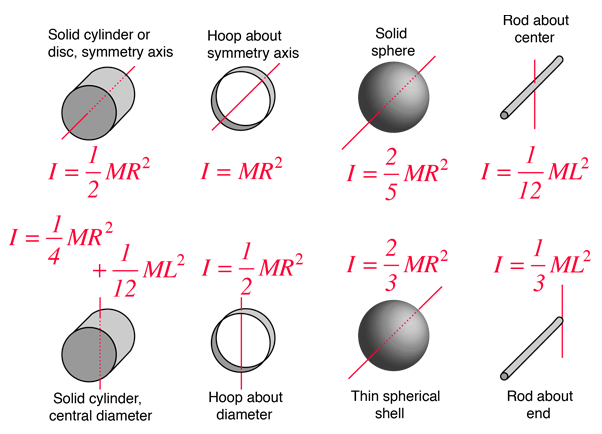 Many symmetries in these objects
Many symmetries in these objects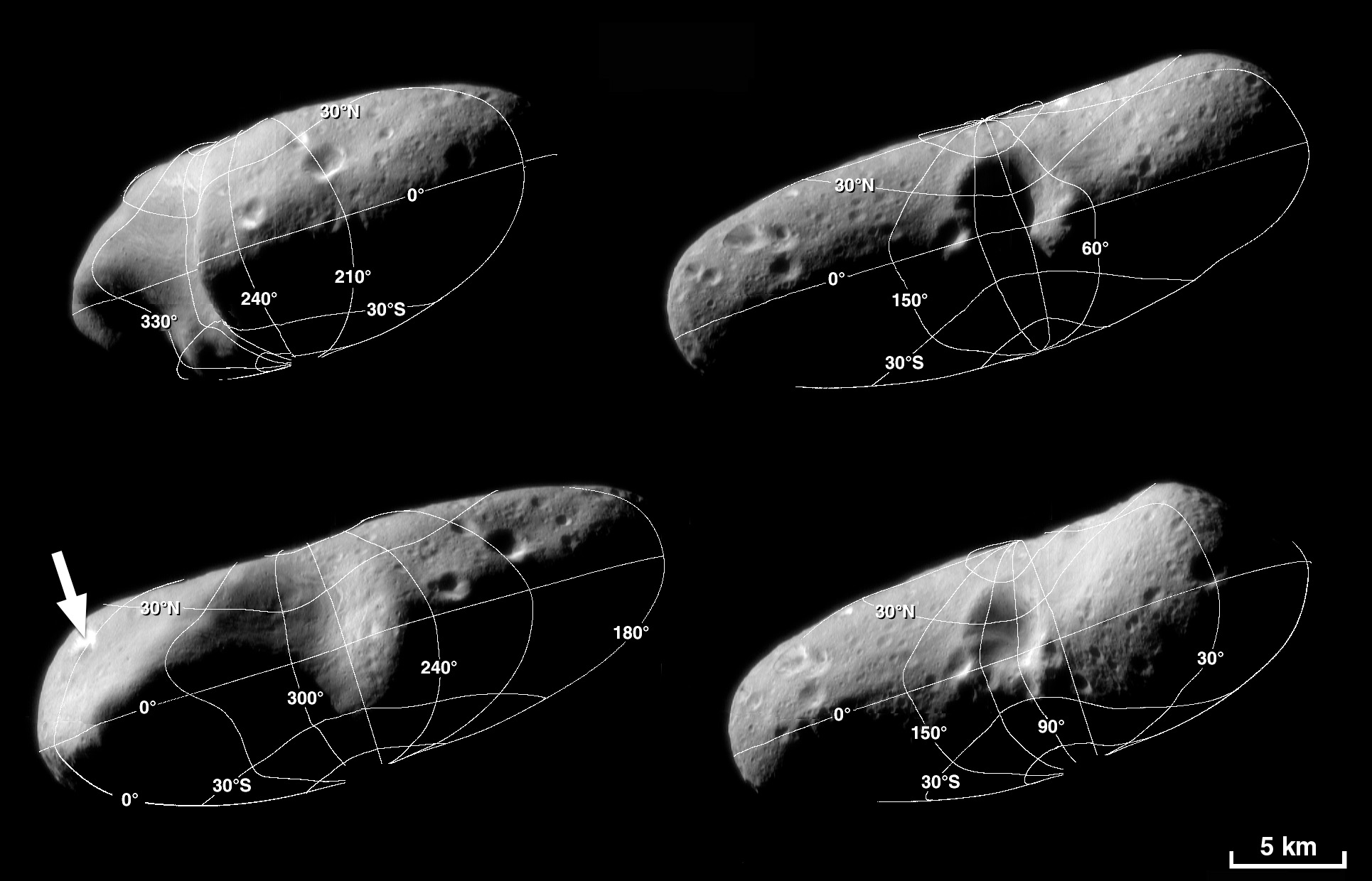 Asteroid Eros, very irregular
Asteroid Eros, very irregular
It is important to remember that potential energy is a property of the interactions between objects in a chosen system, and not just a property of each object.
This will be abstracted in PHY2049, when studying the topic of electrostatic potential, which is defined as a property of a charged object or an array of charged objects. Electrostatic potential is not measured in Joules. It is measured in Volts.
For example, the lowest height in a problem is usually defined as zero potential energy, or if an object is in space, the farthest point away from the system is often defined as zero potential energy
Good to keep in mind, even in PHY2049
This property allows us to define a different kind of energy for the system than its kinetic energy, which is called potential energy.
Recall our discussion in Session 14.1, where we studied
Spring Potential Energy
good workout
39.
Good study problem
38.
Good basic workout
Compare the work required to accelerate a car of mass 2000 kg from 30.0 to 40.0 km/h with that required for an acceleration from 50.0 to 60.0 km/h.
Good workout
Determining a Stopping Force
We worked this problem out in Session 14
By using the work-energy theorem, you did not have to solve a differential equation to determine the height.
True here, but not always the case on a complicated problem.
Loop-the-Loop
A good example to work out
We can also get this result from the work-energy theorem.
This is the primary reason why I refrain from teaching this kinematic equation earlier in a semester
The importance of the work-energy theorem, and the further generalizations to which it leads, is that it makes some types of calculations much simpler to accomplish than they would be by trying to solve Newton’s second law.
A much more interesting way to view the universe.

One very important and widely applicable variable force is the force exerted by a perfectly elastic spring
Extremely important for all scientists
Work Done by a Variable Force over a Curved Path
This example is a little bit unphysical, in that keeping an object on a parabola requires some F = ma. There must be some kind of constraint, like a parabolic track that keeps an object on the track.The external \(\color{red}\vec{F}\) here would be in addition to the constraint forces. So analyzing the forces would be tricky. E.g., you'd also need to know a temporal parameter for the path, which would give you the magnitude of the tangent velocity vector at any time in the path. SO... we will ignore this example!
It is a nice workout, however.
paths
This diagram is slightly blooped up. Path (b) is just the hypotenuse. Path (a), we may assume, is the drop of 1 m folowed by a traverse right of 3 m.
For example, in the rectangular coordinate system in a plane, the scalar x-component of a vector is its dot product with the unit vector ^ii^\mathbf{\hat{i}}, and the scalar y-component of a vector is its dot product with the unit vector ^jj^\mathbf{\hat{j}}:
One can use this idea to compute components of a vector in a new coordinate system (p, q). Just take the dot product of the vector with each new unit vector,
$$\vec{A}\cdot \hat{p}=A_p$$
etc.
We can use the commutative and distributive laws to derive various relations for vectors, such as expressing the dot product of two vectors in terms of their scalar components.
This is a helpful skill to use from time to time: getting products of two vectors in terms of each vector's components.
NASA researchers test a model plane in a wind tunnel. (credit: NASA/Ames)
Mary Jackson, the engineer in Hidden Figures, worked at a wind tunnel just like this one, at NASA/Langley in Virginia. Long may she reign!
A higher coefficient would also allow the car to negotiate the curve at a higher speed
Racing tires are designed to have much larger coefficients of friction, even \(\mu_s >1\).
frictional force
E.g., friction from the road surface on the tires.
In Motion in Two and Three Dimensions, we examined the basic concepts of circular motion. An object undergoing circular motion, like one of the race cars shown at the beginning of this chapter, must be accelerating because it is changing the direction of its velocity. We proved that this centrally directed acceleration, called centripetal acceleration, is given by the formula ac=v2rac=v2r{a}_{\text{c}}=\frac{{v}^{2}}{r} where v is the velocity of the object, directed along a tangent line to the curve at any instant. If we know the angular velocity ωω\omega, then we can use ac=rω2.ac=rω2.{a}_{\text{c}}=r{\omega }^{2}. Angular velocity gives the rate at which the object is turning through the curve, in units of rad/s. This acceleration acts along the radius of the curved path and is thus also referred to as a radial acceleration.
Very nice synopsis for uniform circular motion.
particularly low pressures.
Incorrect. The pressure gradient from the center of a hurricane (maybe 900 millibars) outward to a region of fair weather (1023 millibars), a distance of a few hundred miles, is about 10%, not particularly big, yet it has enormous effects over that distance
we can find the coefficient of kinetic friction if we can find the normal force on the skier
Good
Figure 5.26 The weight of a tightrope walker causes a wire to sag by 5.0∘5.0∘5.0^\circ.
We worked on an asymmetric version of this in Session 11, 9/29/20
Once you have determined the tension in one location, you have determined the tension at all locations along the rope.
Important
outward
.
forces. Zooming in deeper, your body’s atoms are held together by electrical forces, and the core of the atom, called the nucleus, is held together by the strongest force we know—strong nuclear force
There are four fundamental forces in nature:
Forces affect every moment
...of all objects in the universe.
these situations
THE most boring example ever. However, it is valid.
skier
For students from Florida, skiing is a fun physical activity in what we call "mountains" (large piles of rock, thousnads of feet tall), on a cold white slippery substance called "snow," (the crystalline form of \(H_2O\) water). Cf., this skiing area in Montana.

Finding a Particle Acceleration
A good practice problem. You can answer part c with a spreadsheet.
The position of a particle
A nice mini-workout, and you can check your work.
It is remarkable that for each flash of the strobe
Strobe photo, straight drop https://youtu.be/SmEevo_PL7k
This one is not a strobe photo but in slow motion, it ain't bad. https://youtu.be/cxvsHNRXLjw
he velocity vector becomes tangent to the path of the particle.
Enormously important. This is how we define any vector, a tangent vector, so that vectors can be used in curved spacetime. For math fiends, here is nice blurb on manifold tangent vectors.
The instantaneous velocity vector is now
We will actually go to this definition when we study aerodynamic drag forces and terminal velocity.
Brownian Motion
A nice mini-workout, and you can check your work.
The displacement vector Δ→rΔr→\Delta \mathbf{\overset{\to }{r}} is found by subtractin
This is not the same as the three dogs + 1 example from the Ch. 2.3. That resultant vector was a SUM of the first three dogs' pull forces.
This displacement is a DIFFERENCE of two vectors,
$$\Delta\vec{r}=\vec{r}\left(t_2\right)-\vec{r}\left(t_1\right)$$
using vector subtraction, which can be done by
The position vector from the origin of the coordinate system
Make sure to review this part. Vectors are essential.
Thus, to describe the motion of any of the jets accurately, we must assign to each jet a unique position vector in three dimensions as well as a unique velocity and acceleration vector.
We have already seen this in our study of free fall. To integrate the equations of motion (i.e., involving some acceleration, \(\ddot{s}\left(t\right)\)), one needs initial conditions -- initial position and initial velocity.
Our entire program of integration means
A train is moving up a steep grade
We will review this in class on 9/8/20.
Height of free fall
Note the minus sign \(-\frac{1}{2}gt^2\) in the author's version of this formula.
Kinematic Equations for Objects in Free Fall
I hardly ever use the third equation. It is related to conservation of total mechanical energy, which is good, but difficult to use properly, in my opinion.
The equation –v=v0+v2v–=v0+v2\overset{\text{–}}{v}=\frac{{v}_{0}+v}{2} reflects the fact that when acceleration is constant, v is just the simple average of the initial and final velocities.
This is why it works, but only for constant acceleration systems
We now make the important assumption that acceleration is constant.
Just like Galileo did.
Orlando

University of Florida in Gainesville.
A delivery man
Session 1.2 on August 25, 2020, breakout rooms.
scale mode
Another scale model is the "grapefruit model," illustrated nicely in this Youtube:
In the control tower at a regional airport,
Also a good exercise
A barge is pulled by the two tugboats
good exercise
Ask yourself: Does this make any sense?
ALWAYS!!!
If all else fails, bound it. For physical quantities for which you do not have a lot of intuition, sometimes the best you can do is think something like: Well, it must be bigger than this and smaller than that. For example, suppose you need to estimate the mass of a moose. Maybe you have a lot of experience with moose and know their average mass offhand. If so, great. But for most people, the best they can do is to think something like: It must be bigger than a person (of order 102 kg) and less than a car (of order 103 kg). If you need a single number for a subsequent calculation, you can take the geometric mean of the upper and lower bound—that is, you multiply them together and then take the square root. For the moose mass example, this would be
Helpful when doing mental arithmetic. You get skilled with this, you can beat people on calculators!
This simple fact can be used to check for typos or algebra mistakes, to help remember the various laws of physics, and even to suggest the form that new laws of physics might take.
"Checking the units" is a simple check on your derivations and solutions. Very important
yotta
Based on another familiar term. ; )
Check out a comprehensive source of information on SI units at the National Institute of Standards and Technology (NIST) Reference on Constants, Units, and Uncertainty.
Well worth checking out.
base units. All other physical quantities can then be expressed as algebraic combinations of the base quantities. Each of these physical quantities is then known as a derived quantity and each unit is called a derived unit.
The distinction between base units and derived units is important.
the units for some physical quantities must be defined through a measurement process
This is significant.
Amount of substance mole (mol)
Derived from Latin mole, meaning bulk in English.<br> Cf., definition of molecule.
The metric system is also the standard system agreed on by scientists and mathematicians.
We will mostly use metric units in PHY2048.
Mathematical Formulas
We will be using a ton of these formulas, even the series expansions.
Newton’s Law of Gravitation
Check your numbers: [h5p id="1"]
For a star 500 light-years away, the light we detect tonight left 500 years ago and is carrying 500-year-old news.
Electromagnetic waves carry energy, momentum and information!
Given that maximum air displacements are possible at the open end and none at the closed end, other shorter wavelengths can resonate in the tube
Boundary conditions are determined by the physical factors like length etc. You will find this all over physics!!
ear. This wave function models the displacement of the medium of the resulting wave at each position along the x-axis. If two linear waves occupy the same medium, they are said to interfere.
Interference!!!!
to a linear restoring force of the medium
Linear restoring force means porportional to displacement \(x\), like the spring force \(\vec{F}=-kx\left(\hat{i}\right)\).
However, because the Taylor series exists, we can cobble together a linear wave equation from a nonlinear system, like the fluid we call air, for "small" displacements away from the equilibrium at ambient atmospheric pressure.
linear wave equation
the relation \(\frac{\omega^2}{k^2}=v^2\) is known as a dispersion relation.
partial derivative
Have you learned about partial derivatives yet?
the wave speed is constant and represents the speed of the wave as it propagates through the medium, not the speed of the particles that make up the medium
Important distinction. The medium moves about equilibrium, but the wave energy and momentum move through the medium.
A wave function is any function such that
This is why there is a famous differential equation, the "one-way wave equation," viz. $$\frac{df}{dt}-v\frac{df}{dt}=0$$
Whether the temporal term ωtωt\omega t is negative or positive depends on the direction of the wave.
$$\frac{d}{dt}\varphi=\frac{d}{dt}\left(kx-\omega t\right)=k\frac{dx}{dt}-\omega$$
$$kv-\omega=0\text{ since }\varphi\text{ is a constant}$$
This means that the velocity of the phase \(\varphi\) is \(v=\frac{\omega}{k}=\lambda f\) since \(k=\frac{2\pi}{\lambda}\).
Then consider \(\varphi=kx+\omega t\) instead. That would correspond to a leftward propagating wave, as the text mentions.
16.6 Standing Waves and Resonance
Check out some of the resonance and standing wave demonstrations in my Demonstrations playlist in YouTube.
Waves may be transverse, longitudinal, or a combination of the two.
Read this paragraph
waves on stringed instruments
In a longitudinal wave
like sound waves
This fundamental relationship holds for all types of waves.
Even the nastiest physical system one could imagine, like the plasma states of the atmosphere of the Sun, when you comb through the calculus and extreme geometry, you can still make out wave equations like this one, \(v=\lambda f\)

the equilibrium position is indicated by the dotted line
I.e., sea level!
The amplitude of the wave (A) is a measure of the maximum displacement of the medium from its equilibrium position.
Or, in the case of sound waves, from its equilibrium pressure state -- the ambient atmospheric pressure.
Matter waves are a central part of the branch of physics known as quantum mechanics.
You might get to quantum waves in PHY2049 or PHY3101 or higher courses.
Electromagnetic waves are associated with oscillations in electric and magnetic fields and do not require a medium.
You will study these in PHY2049.
vibrating tuning fork
Check this video in YouTube with two tuning forks.
For sound waves, the disturbance is a change in air pressure
Very complex time evolution equations for pressure, but they boil down under certain conditions to linear wave equations for the pressure as a function of position and time, \(p\left(x,\, t\right)\)
Mechanical waves transfer energy and momentum
Transport of energy and momentum across spacetime.
elastic restoring forc
Why we study oscillation in the simple spring-mass system, \(\vec{F}\left(x\right)=-kx\left(\hat{i}\right)\)
34. One type of BB gun uses a spring-driven plunger to blow the BB from its barrel. (a) Calculate the force constant of its plunger’s spring if you must compress it 0.150 m to drive the 0.0500-kg plunger to a top speed of 20.0 m/s. (b) What force must be exerted to compress the spring?
good workout involving max speed
32. Fish are hung on a spring scale to determine their mass. (a) What is the force constant of the spring in such a scale if it the spring stretches 8.00 cm for a 10.0 kg load? (b) What is the mass of a fish that stretches the spring 5.50 cm? (c) How far apart are the half-kilogram marks on the scale?
Good workout
A suspension bridge oscillates with an effective force constant of 1.00×108N/m1.00×108N/m. (a) How much energy is needed to make it oscillate with an amplitude of 0.100 m? (b) If soldiers march across the bridge with a cadence equal to the bridge’s natural frequency and impart 1.00×104J1.00×104J of energy each second, how long does it take for the bridge’s oscillations to go from 0.100 m to 0.500 m amplitude.
Nice workout
15.6 Forced Oscillations
Bypass for now. Physics and engineering majors will see plenty of instruction on forced oscillation in upper level courses.
15.5 Damped Oscillations
Bypass for now. Physics and engineering majors will see plenty of instruction on damped oscillation in upper level courses.
if you are familiar with
Another way to think about this approximation is the Taylor series for a function \(f\left(x\right)\) near its minimum at \(x = a\).
$$f\left(x\right)\approx f\left(a\right)+f^{\prime}\left(a\right) \left(x-a\right)+\frac{1}{2}f^{\prime\prime}\left(a\right)\left(x-a\right)^2$$
At the minimum, the derivative is zero, so \(f^{\prime}\left(a\right)=0\). Therefore, the first order term drops out; the zeroth order term, \(f\left( a\right)\) and the second order term \(\frac{1}{2}f^{\prime \prime}\left(a\right)\left(x-a\right)^2\) remain, i.e.,
$$f\left(x\right)\approx f\left(a\right)+\frac{1}{2}f^{\prime\prime}\left(a\right)\left(x-a\right)^2$$
If the function \(f\) is your potential, then you now have an oscillator potential for this small neighborhood of \(x=a\). We know the solutions for \(x\left(t\right)\) in this neighborhood, as we discussed in remote session 26.
Many physical systems can be studied profitably from this standpoint, the Taylor series expansion of the potential near one of its minima.
energy proportional to the amplitude squared
In the electromagnetic field of electric field \(\vec{E}\) and magnetic field \(\vec{B}\), the energy density of the field, \(u\), is also proportional to the squares of the fields: $$u=\frac{1}{2}\epsilon_0E^2+\frac{1}{2}\frac{1}{\mu_0}B^2$$
The constants \(\epsilon_0\) and \(\mu_0\) are related to the speed of light \(c\) :
$$c^2=\frac{1}{\epsilon_0 \mu_0}$$
can be approximated
after a ton of algebra
the atoms can be separated
molecule broken
when displaced a small amount from the equilibrium position.
the famous case of "small" displacements.
A practical application of the concept of stable equilibrium points is the force between two neutral atoms in a molecule.
Entree to current research areas!
The potential energy curve in Figure resembles a bowl.
good
is proportional to the square of the amplitude
Because, when \(x=\pm A\), the kinetic energy is zero, no matter what your initial conditions were, and all the energy \(E\) is potential.
Energy in Simple Harmonic Motion
The heart of the matter
Using the small angle approximation gives an approximate solution for small angles,
"small"
new equilibrium position
$$y_1$$
The spring is hung from the ceiling and the equilibrium position is marked as yoyo{y}_{o}.
with only the mass of the spring
Vertical Motion and a Horizontal Spring
Cancelling out like terms
Uh oh. The Math Dept. would not approve!

equations of motion and Newton’s second law
I.e., use a differential equation based on \(F=m\ddot{x}\).
The position, velocity, and acceleration can be found for any time.
...as usual with equations of motion!
can be modeled with the following equations of motion:
Alternate model uses the generic solution but with the phase \(\phi\) converted into a sine term. E.g.,
$$x\left(t\right)=a\, \cos\left(\omega t\right)+b\, \sin\left(\omega t\right)$$
The constants \(a\) and \(b\) look like components of a vector whose magnitude is \(A\), viz. $$a=A\cos\left(\varphi\right) \ b=-A\sin\left(\varphi\right)$$

pulling it out to x=+0.02m.x=+0.02m.x=+0.02\,\text{m}\text{.} The block is released from rest
Initial conditions easiest to use: $$x\left(0\right)=0.02\, m \ \dot{x}\left(0\right)=0.0\frac{m}{s}$$
Result: \(\varphi = 0\). Nice.
The velocity of the mass on a spring, oscillating in SHM, can be found by taking the derivative of the position equation
We know this already
This is the generalized equation for SHM
Good.
Figure 15.6
The velocity is leftward, derivative is negative, $$\dot{x}<0$$ during the first half of the motion, then rightward, positive derivative, $$\dot{x}>0$$ in the second half of the cycle... from THESE initial conditions $$x\left(0\right)=A\ \dot{x}\left(0\right)=0$$
Figure 15.5
This figure is a nice synopsis
repeats every integer multiple of the period.
That is, when \(t=T,\,2T,\,3T\dots\)
from rest
so the work done is not in KE, it is in the potential energy.
analyze the equations of motion
✔︎
For one thing, the period T and frequency f of a simple harmonic oscillator are independent of amplitude.
I think we demonstrated this with variation of the swing angle back when we used pendula in the classroom.
The stiffer the spring is, the smaller the period T. The greater the mass of the object is, the greater the period T.
We already know this from earlier in the semester: $$\omega^2=\frac{k}{m}$$
The mass now begins to accelerate in the positive x-direction
Incorrect. Its acceleration is rightward as soon as it crosses equilibrium, \(x<0\), i.e., in (c).
maximum negative velocity at x=0x=0x=0.
also max KE
The mass is displaced to a position x=Ax=Ax=A and released from rest.
Initial conditions: $$\vec{F}\left(0\right)=kA\left(-\hat{i}\right)$$ $$x\left(0\right)=A$$ $$\vec{v}\left(0\right)=0$$
In simple harmonic motion, the acceleration of the system, and therefore the net force, is proportional to the displacement and acts in the opposite direction of the displacement.
These words imply, as we have already seen, that the total energy \(E\) is proportional to the square of the displacement, \(q\), using a generic coordinate \(q\) and to the square of the coordinate velocity, \(\dot{q}\). Or, as the math department might say, the function \(E\) is "quadratic" in \(q\) and \(\dot{q}\).
much highe
$$\frac{\text{human}}{\text{ultra}}=\left(2\times 10^4\right)/ \left(2.5\times 10^6\right)\approx 0.01$$
So that is "small" in the sense of calculus shortcuts.
This also means the wavelengths are much smaller for ultrasound.
Period and Frequency in Oscillations
Basic terms, must be familiar with them and where they fit into the equations of motion.
Damping
Dissipates energy.
This is the weight of a typical grain of pollen.
Cavendish, however, could measure quantities like this!
Cavendish determined it to be
actually in Cavendish's day, it was $$G=6.754\times 10^{-11}N\,m^2/kg^2$$
for objects within a few kilometers of Earth’s surface, we can take
"a few kilometers"
I.e., from the top of Mt. Everest (elevation \(\approx 9\, km\)) to the bottom of the Mariana Trench (depth \(\approx 11\, km\). Cf., NASA planetary fact sheet.
E.g., $$\text{Everest} \longrightarrow\frac{1}{6380^2}=\frac{1}{40704400}\approx 2.457\times 10^{-8}$$ $$\text{sea level}\longrightarrow\frac{1}{6371^2}=\frac{1}{40589641}\approx 2.464\times 10^{-8}$$ $$\text{Challenger Deep}\longrightarrow\frac{1}{6360^2}=\frac{1}{40449600}\approx 2.472\times 10^{-8}$$
the radius of Earth
Not true for the Earth-moon system, as discussed, but good for most terrestrial objects like the oceans and for human objects like stadia and great pyramids.
Earth-moon system:

Earth and the average depth of the ocean (blue line):

Spectrum stadium, a blip next to Earth itself:

will be cancelled
due to the symmetry of the circle of radius \(R_i\)
the magnitude of the angular momentum of this mass segment is
i.e., the orbital angular momentum of a single pixel
small mass segments
pixellation