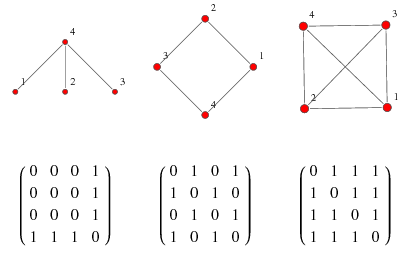
19. Y. Lin, R. Jin, D. Cai, S. Yan, X. Li, in 2013 IEEE Conference on Computer Vision and Pattern Recognition (IEEE Computer Society, 2013), pp. 446–451.
Lin et al. address a known issue in hashing methods, which is that they often require a large number of hash tables to be effective.
To solve this problem, the authors propose a novel approach called compressed hashing. This approach uses sparse coding and is shown to be more effective than previously known hashing algorithms.