The fixed filing place needs no system. It is sufficient that we give every slip a number which is easily seen (in or case on the left of the first line) and that we never change this number and thus the fixed place of the slip. This decision about structure is that reduction of the complexity of possible arrangements, which makes possible the creation of high complexity in the card file and thus makes possible its ability to communicate in the first place.
There's an interesting analogy between Niklas Luhmann's zettelkasten numbering system and the early street address system in Vienna. Just as people (often) have a fixed address, they're able to leave it temporarily and mix with other people before going back home every night. The same is true with his index cards. Without the ability to remove cards and remix them in various orders, the system has far less complexity and simultaneously far less value.
Link to reference of street addressing systems of Vienna quoted by Markus Krajewski in (chapter 3 of) Paper Machines.
Both the stability and the occasional complexity of the system give it tremendous value.
How is this linked to the idea that some of the most interesting things within systems happen at the edges of the system which have the most complexity? Cards that sit idly have less value for their stability while cards at the edges that move around the most and interact with other cards and ideas provide the most value.
Graph this out on a multi-axis drawing. Is the relationship linear, non-linear, exponential? What is the relationship of this movement to the links between cards? Is it essentially the same (particularly in digital settings) as movement?
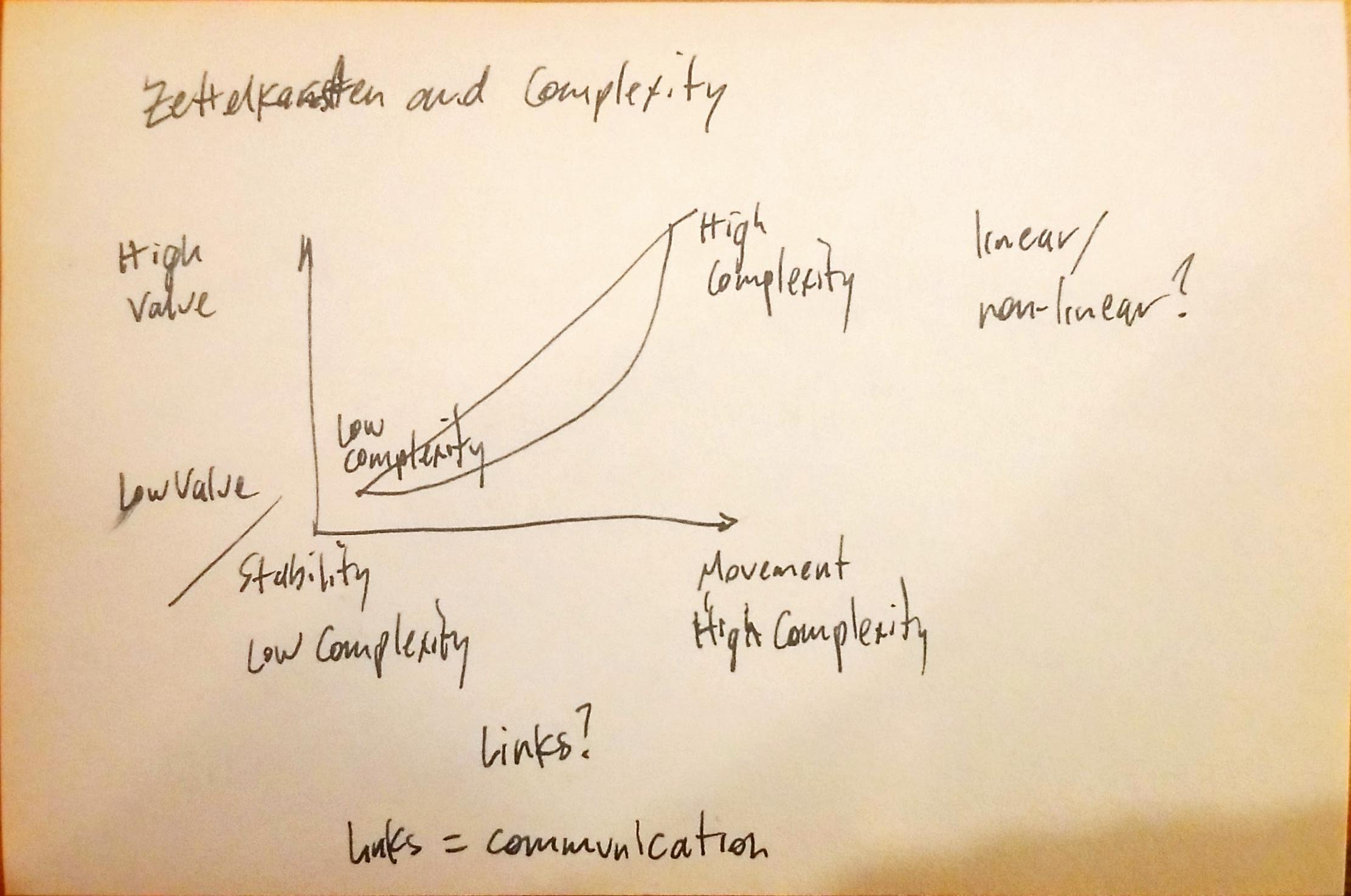
Are links (and the active creation thereof) between cards the equivalent of communication?