- Nov 2023
-
www.resilience.org www.resilience.org
-
shallow article but worth taking a look at the main point: sand usage. There's a diff depending on use / location etc.
-
- Oct 2023
-
-
Mit drastischen Repressionsmaßnahmen versuchte die Polizei, Proteste gegen die Internationale Automobilausstellung IAAA in München zu unterdrücken. Verdächtig wirkende Personen wurden in der Stadt festgehalten und durchsucht, während der Automobiliindustrie große Flächen als „open spaces“ zur Veerfügung gestellt wurden. Dennoch erregten Proteste und Aktionen große öffentliche Aufmerksamkeit. https://taz.de/Protest-gegen-Automobilausstellung-IAA/!5956556/
-
- Aug 2022
-
www.youtube.com www.youtube.com
-
If I'm not mistaken, this is the original song which C.J. Craig sings a portion of in the Red Haven's on Fire episode of The West Wing. https://www.imdb.com/title/tt0745672
Tags
Annotators
URL
-
- Apr 2022
-
-
Wax tablets were the standard erasable surfacefrom antiquity to the Renaissance: one or more boards, often bound togetherin a codex form, were coated in wax to be inscribed with a stylus then erased forreuse.7 In early modern England one could also purchase pocket-sized writingtablets featuring paper that had been treated so as to offer a rigid writing surfaceon which markings made with the accompanying metal stylus could be erasedwith a little moisture.8 The slate blackboard is also attested in Europe in musicinstruction in the sixteenth century, sized either for group or for personal use(as is still the case today), and was used at least by the eighteenth century in theteaching of astronomy. The sand tray, a board or slab spread with a fine layer ofsand that one inscribed with a stick and could easily erase, was another long-lived medium: used in ancient Babylon and medieval Islam for calculations andin Europe principally for children and artists learning to write or sketch down tothe Victorian period.9 None of these temporary notes have left any traces, exceptthrough extant higher- order notes made from them.
-
- Dec 2017
-
www.sacred-texts.com www.sacred-texts.com
-
1.
Assumption 1: The Earth is no bigger than 529,200 km round. (I converted it from his 3,000,000 stadia.) This means that the radius of this "no bigger than" Earth is 84,225 km.
-
I suppose the diameter of the sun to be about 30 times that of the moon and not greater.
Again, Archimedes is saying, "You can't say my numbers are too small. I will take the biggest estimate and then make the one I use even bigger."
-
Pheidias
We know very little about this Phidias. Some think he was Archimedes' actual father and others think he was only a teacher that Archimedes thought of as a father-figure.
-
King Gelon
-
Sicily
Google Earth of Sicily, now a part of Italy. But, in Archimedes' time considered part of "Magna Graecia"
-
Again there are some who, without regarding it as infinite, yet think that no number has been named which is great enough to exceed its multitude.
Archiomedes' main reason for writing the Sand Reckoner is not so that he can get an accurate estimate of the number of sands in the Universe. It is so that he can put forth his arguments about the number system the Greeks used at this time and how that system should deal with very large numbers. The Greeks knew about the concepts of zero and infinity and even negative numbers. But, they rejected them as things that should be used in math. Archimedes is making his case for very large numbers.
-
Zeuxippus
Zeuxippus was the immediate successor to Euclid as a mathematics professor at Alexandria and a correspondent with Archimedes during his life. From Wikisource.org
-
universe
"A term for "universe" among the ancient Greek philosophers from Pythagoras onwards was τὸ πᾶν tò pân ("the all"), defined as all matter and all space, and τὸ ὅλον tò hólon ("all things"), which did not necessarily include the void." from Wikipedia.org
Image from UCR.edu -
Aristarchus
Aristarchus of Samos
Source: Wikimedia.org -
Samos
Google Earth link to the Island of Samos.
-
a book consisting of some hypotheses
The book was called On the Sizes and Distances.
-
His hypothese
Image is fron an excellent article on Aristarchus' theories at AncientGreeceReloaded.com. (Use google translate to translate text to English.)
-
proportion
For my GHF class "Aristotle Leads the Way" notice the use of our friend for the year: proportionality.
Image is from a great article on proportionality at ExamRefresh.com -
We must however take Aristarchus to mean this: since we conceive the earth to be, as it were, the centre of the universe, the ratio which the earth bears to what we describe as the 'universe' is the same as the ratio which the sphere containing the circle in which he supposes the earth to revolve bears to the sphere of the fixed stars.
It's really hard to understand what he is saying here. So, most scholars use the description of the math below to figure out what he meant to say here.
-
some exceed in multitude the number of the sand which is equal in magnitude to the sphere referred to
Archimedes is saying that he will prove that he has thought up numbers that are bigger than the number of sands in the Universe. Unfortunately, we have lost all copies of his work called "The Principles" that he is referring to. So, we use this work to talk about Archimedes' very large numbers until we find a copy of that original work (if one still exists).
-
some have tried, as you are of course aware, to prove that the said perimeter is about 300,000 stadia
Archimedes' good friend Eratosthenes is the person who has estimated the perimeter of the Earth to be about 300,000 stadia. Eratosthenes actually said that the circumference of the Earth was 252,000 stadia which converts to about 44,452.8 km. The actual value of the polar (north-south) circumference of the Earth is approximately 39,940.6 km. While this yields a 10% error it was a vastly superior estimate than any other we have a record of from a 1,000 years before or after Eratosthenes.
-
ten times the size that my predecessors thought it
Is Archimedes saying his good friend, Eratosthenes was wrong? Not really. He is saying, "Look, I don't want you to criticize my number as too small. So, let's put the Earth at 10 times the current estimate just to prove my point..."
-
Eudoxus
Eudoxus said that the Universe was made of a system of spheres.
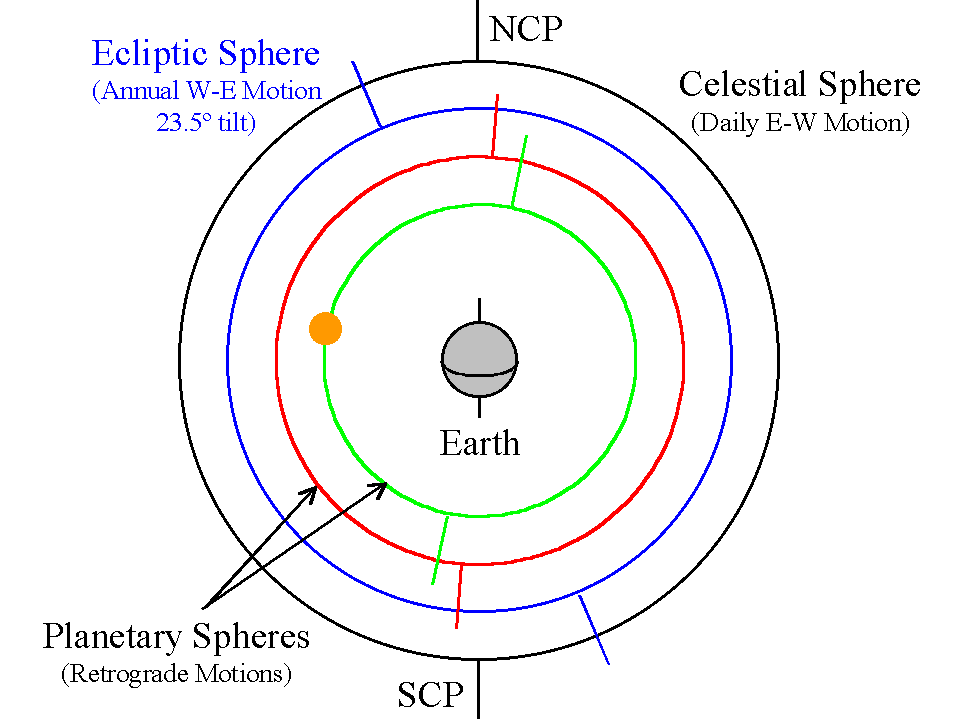Image Credit: Prof. Richard Pogge, Ohio State
-
- Sep 2017
-
blog.jonudell.net blog.jonudell.net
-
lisskane her grain of sand, dackolupatoni
my favorite grain of sand
-
-
blog.jonudell.net blog.jonudell.net
-
Grains of sand are inert physical objects. They just lie around
against the inherent laziness of sand
-
