Authors contact
this part should only be printed out in docx rendered output
Authors contact
this part should only be printed out in docx rendered output
The authors declare no conflicts of interest.
R packages
add patchwork and grateful
what we are saying is we do not know how the soul generates the intelligence it clearly has but that it has it is obvious it doesn't divide until it knows that the genome has been accurately replicated
for - cell intelligence - the cell knowns when to divide - it won't divide until all replication errors have been fixed
harmonically this is pretty straightforward we're in the key of E minor right now and I've got the e natural minor scale loaded up on the accordion
So excited to see aQWERTYon allows you to set to a key and a major/minor tonality, in this case E minor. This means the base note (bottom-left, Z) is E as the tonic of the E minor. This allows for both fixed do naming of actual notes (without needing to hear the nice music transposed) and at the same time analyze the music and chords FUNCTIONALLY (in the movable do sense). Truly the best of both worlds!
It's a fork of Memery gem. Original Memery uses prepend Module.new with memoized methods, not touching original ones. This approach has advantages, but also has problems, see discussion here: tycooon#1
Then again, at times the little steel“dog” with its escapement working backand forth in the ratchet which controlledthe movement of the paper frame wouldfail to do its work properly, and the car-riage would jump an inch or two, or per-haps half a line, stopping with a suddenjerk, which was calculated to make onenervous, to say the least.
Apparently they were calling it a "dog" pretty early on...
And this is what I believe is happening with students and reading, at least in part. They have convinced themselves that they aren’t readers. They have convinced themselves that reading old books, especially difficult old books, is just too arduous, too boring, too pointless. They have convinced themselves that even if the books are good and soul-enriching, there are better things to be doing with their time.
Fixed mindset. Self fulfilling prophecies. Ignorance.
Enable ActiveRecord unsigned integers to use 8 bytes instead of 4. This fixes the ActiveModel::RangeError problem where AR models with perfectly fine 8 bytes primary keys are taken for ActiveModel::Type::Integer with a default limit of 4 bytes.
I'm going to close this thread which will no longer be monitored. In case you want to report a new issue or you can’t make project to be internal, please do not hesitate to create a new Issue Tracker thread describing your situation.
Windows 10 currently (01.01.2020) doesn't support Unicode country flags, and displays two-letter country codes instead of emoji flag images.
Stop autoclosing of PRs While the idea of cleaning up the the PRs list by nudging reviewers with the stale message and closing PRs that didn't got a review in time cloud work for the maintainers, in practice it discourages contributors to submit contributions. Keeping PRs open and not providing feedback also doesn't help with contributors motivation, so while I'm disabling this feature of the bot we still need to come up with a process that will help us to keep the number of PRs in check, but celebrate the work contributors already did instead of ignoring it, or dismissing in the form of a "stale" alerts, and automatically closing PRs.
Yes!! Thank you!!
typo: cloud work -> could work
I don't understand why it should be so hard to keep issues open / reopen them. That's just going to cause people to open a duplicate issue/PR — or (if they notice in time) cause people to add extra "not stale" noise when the bot warns it's about to be closed. Wouldn't it be preferable to keep the discussion together in one place instead of spreading across duplicate issues? (Similarly, moving the meta conversation about an issue out to a completely separate system (Discord) seems like the wrong direction, because it wouldn't be visible to/discoverable by those arriving at the closed issue.) I get how it's useful to have stale issues not cluttering the list. But if interes/activity later picks up again, then "stale" is no longer accurate and its status should be automatically updated to reflect its newfound freshness... like it did back here:
Rails 7 supports Postgres enums natively (more info)
The fixed filing place needs no system. It is sufficient that we give every slip a number which is easily seen (in or case on the left of the first line) and that we never change this number and thus the fixed place of the slip. This decision about structure is that reduction of the complexity of possible arrangements, which makes possible the creation of high complexity in the card file and thus makes possible its ability to communicate in the first place.
There's an interesting analogy between Niklas Luhmann's zettelkasten numbering system and the early street address system in Vienna. Just as people (often) have a fixed address, they're able to leave it temporarily and mix with other people before going back home every night. The same is true with his index cards. Without the ability to remove cards and remix them in various orders, the system has far less complexity and simultaneously far less value.
Link to reference of street addressing systems of Vienna quoted by Markus Krajewski in (chapter 3 of) Paper Machines.
Both the stability and the occasional complexity of the system give it tremendous value.
How is this linked to the idea that some of the most interesting things within systems happen at the edges of the system which have the most complexity? Cards that sit idly have less value for their stability while cards at the edges that move around the most and interact with other cards and ideas provide the most value.
Graph this out on a multi-axis drawing. Is the relationship linear, non-linear, exponential? What is the relationship of this movement to the links between cards? Is it essentially the same (particularly in digital settings) as movement?
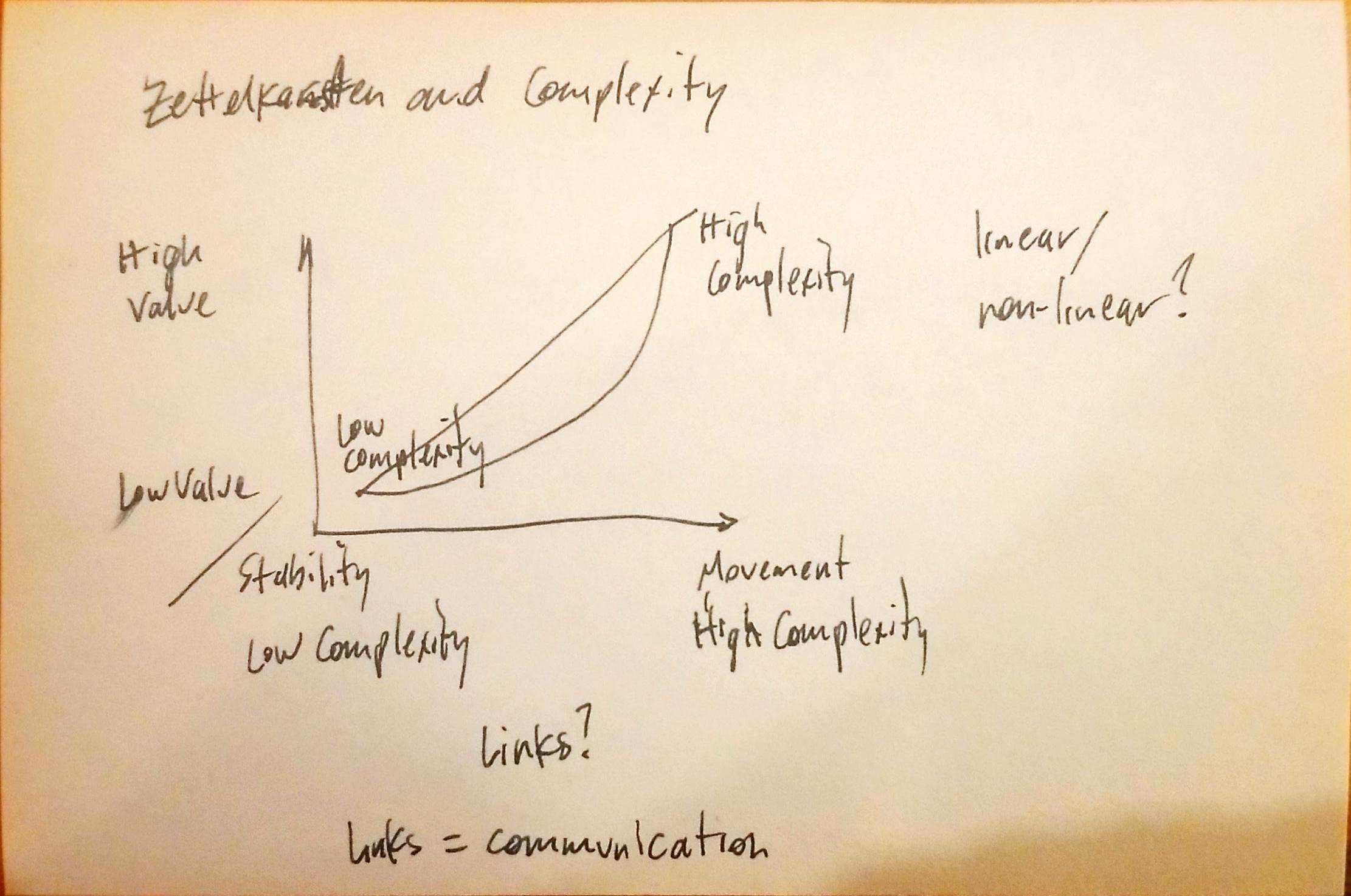
Are links (and the active creation thereof) between cards the equivalent of communication?
Rails' inability to automatically route my link_to and form_for in STI subclasses to the superclass is a constant source of frustration to me. +1 for fixing this bug.
I've had to work around this by doing record.as(BaseClass)
Closing this PR since it's been sitting here for over 2 years. Can reopen if need be.
Happy Third Birthday #24728!
Closing this because it's obviously not going to get fixed and it's cluttering my open issues
17.3. Fixed point
QUESTION: What is a fixed-point of a function?
ANSWER: See this video) at least, and the Fixed-point (mathematics)) wikipedia article:
In mathematics, a fixed point (sometimes shortened to fixpoint, also known as an invariant point) of a function is an element of the function's domain that is mapped to itself by the function. That is to say, c is a fixed point of the function
fiff(c) = c. This meansf(f(...f(c)...)) = f n(c) = can important terminating consideration when recursively computing f. A set of fixed points is sometimes called a fixed set.
For example, if f is defined on the real numbers by
f(x)=x^{2}-3x+4,}, then 2 is a fixed point off, becausef(2) = 2.
There is also the wiki article fixed-point combinator that actually plays a role here, but read through the articles in this order.
Then dissect the Stackoverflow thread What is a Y combinator?, and pay attention to the comments! For example:
According to Mike Vanier's description, your definition for Y is actually not a combinator because it's recursive. Under "Eliminating (most) explicit recursion (lazy version)" he has the lazy scheme equivalent of your C# code but explains in point 2: "It is not a combinator, because the Y in the body of the definition is a free variable which is only bound once the definition is complete..." I think the cool thing about Y-combinators is that they produce recursion by evaluating the fixed-point of a function. In this way, they don't need explicit recursion. – GrantJ Jul 18 '11 at 0:02
(wut?)
Other resources in no particular order:
QUESTION: How the hell did they come up with the idea of using this with Nix and package management? (..and who? I remember a video saved somewhere, but maybe that was about overlays)
QUESTION: ... and how does it work in this context?
ANSWER: Well, not an answer yet, but this may be something in the right direction:
http://blog.tpleyer.de/posts/2020-01-29-Nix-overlay-evaluation-example.html
Can you re-open this until we fix it?
Covid-19 has decimated independent U.S. primary care practices—How should policymakers and payers respond? (2020, July 2). The BMJ. https://blogs.bmj.com/bmj/2020/07/02/covid-19-has-decimated-independent-u-s-primary-care-practices-how-should-policymakers-and-payers-respond/
Lyons, Richard K, and Ganesh Viswanath-Natraj. ‘What Keeps Stablecoins Stable?’ Working Paper. Working Paper Series. National Bureau of Economic Research, May 2020. https://doi.org/10.3386/w27136.
The typical clinical course of an epidural hematoma is an initial loss of consciousness, a lucid interval, and recurrent loss of consciousness with an ipsilateral fixed and dilated pupil. While decompression of subdural hematomas may be delayed, epidural hematomas require evacuation within 70 minutes.
Unlike similar tools that are scheduled to take backups at a fixed time of the day, Timeshift is designed to run once every hour and take snapshots only when a snapshot is due. This is more suitable for desktop users who keep their laptops and desktops switched on for few hours daily. Scheduling snapshots at a fixed time on such users will result in missed backups since the system may not be running when the snapshot is scheduled to run. By running once every hour and creating snapshots when due, Timeshift ensures that backups are not missed.
fixed-point
"fixed-point", "fix point" seems to be most important concept in Nix, because overrides, overridePackages, overlays are built using it.
This model of microservices that register themselves to a global registry will have a lot of advantages when it comes to building one or multiple applications using a microservice architectural approach. Eureka on its own won't have that much of use, but as you'll see in the future blogposts, Eureka will be the key element to locate all of our microservices.
How to use Eureka locate our microservices?
all Eureka clients register itself in the register center(Eureka Server)