(11.11) This feels like an example where ritual is broken for the virtues of humanity and respect. The students are almost like sons to The Master, so they show a sort of filial piety onto him. Yet, they still have moral and social allegiance to their peer. I find it interesting that Confucius ideas have rules not in writing but in feeling and respect
- Last 7 days
-
drive.google.com drive.google.com
-
ibestuur.nl ibestuur.nl
-
Microsoft circumvented a 2023 ban on big data centers in Amsterdam / North-Holland, by splitting the permit process up in three separate ones. Despite it all using a single connection to the grid.
-
-
gitlab.huma-num.fr gitlab.huma-num.fr
-
On fait une vérification avec 20 labels test. Si ces 20 labels sont déjà présents dans la base alors le modèle d'embeddings est le même.
expliquer ?
-
Sur la première ligne du fichier collection il faut également indiquer le lien Hugging Face du modèle à utiliser.
?
-
collections
gitignored !
-
à ses deux dernières lignes
??
-
En utilisant les bases fournies pour la construction d'un service de réconciliation l'idée était de permettre
pas clair ; parler au présent
-
Cette documentation ne s'intéressera pas à l'usage classique de openrefine-wikibase. Pour des informations à ce sujet se référer à la documentation du répository mentionné précedement.
reformuler
-
-
open.library.okstate.edu open.library.okstate.edu
-
Adapt your writing to meet the needs, interests, culture, and background of those who will be reading your documents.
This statement stuck out to me because I feel as though many writers don't keep the readers in mind when they have a story to tell.Usually they convey the message in the most easiest way they know how but this might not grab your readers attention. Thinking about what interest your audience will make your writing stand out.
-
-
www.biorxiv.org www.biorxiv.org
-
Version 3 of this preprint has been peer-reviewed and recommended by Peer Community in Genomics.<br /> See the peer reviews and the recommendation.
-
Version 3 of this preprint has been peer-reviewed and recommended by Peer Community in Genomics.<br /> See the peer reviews and the recommendation.
-
-
sacred-texts.com sacred-texts.com
-
but if one single tear bedews her cheek, she is no longer strong in the sanctity of her vow.
emotions such as crying are seen as a moral failure.
-
There are women who are too diffident, and too reserved, and carry their generosity to such an extent as to pretend not to be aware even of such anoyances as afford them just grounds of complaint.
endurance is framed as weakness rather than restraint and that is very interesting
-
A girl whom we thus educate, and who proves to be competent to bear us company, often disappoints us when she is left alone.
virtue appears stable only under male supervision
-
She is not only incapable of sharing these with him, but might carelessly remark, "What ails you?" How severely would this try the temper of a man
male irritation
-
As for the lower class, it would be almost useless to trouble ourselves with them."
a blunt statement regarding court hierarchy
-
But how often such girls as these are conceited about their own accomplishments, and endeavor unduly to disparage those of others!
shows that female talent is admired but also distrusted/ distasteful when the woman themself is self aware of the talent.
-
"how difficult it is to meet with a fair creature, of whom one can say, ‘This is, indeed, the one; here is, at last, perfection.’ There are, indeed, many who fascinate; many who are ready with their pens, and who, when occasion
romantic dissatisfaction is framed as an inevitable condition.
-
And so all stiffness and formality were dispensed with, and they did not scruple to reveal their secrets to each other.
break from court etiquette.
-
His father-in-law naturally felt for him, and his sons were sent to bear him company.
family obligation and sympathy.
-
He had always striven to keep all these intrigues in the utmost secrecy, and had to appear constantly virtuous. This caution was observed to such an extent that he scarcely accomplished anything really romantic, a fact which Katano-no-Shiôshiô 1 would have ridiculed.
He was so discrete that he undermined his passion as well.
-
Hikal Genji—the name is singularly well known, and is the subject of innumerable remarks and censures.
clearly they are well known, seems that he is both admired and criticised.
-
-
books.stre.bz books.stre.bz
-
slide-based evaluation
Typo: "slice-based evaluation"
-
-
Local file Local file
-
A medium utilised for excapism and propaganda, the cinema was an integral part of the home front experience for most in Britain and Germany, analysis of the sort of movies produced and their reception suggesting that civilians experience of this form of 'entertainment' was more similar than first believed.
Noting that (stats), the cinema was a significant source of excapism during the war, cinema's re-opened despite fears of bombing. monitered by the (), Britain, like Germany, saw films censorship. Nevertheless, while Germany saw hollywood films banned entirely by (), British audiences were still able to () hollwood blockbusters, (historian) noting how they reigned supreme in places like portsmouth. Nevertheless, like Germany, National productions were typically popular, the MO noting an increased desire for comedies and romances as the time went on. As such, we could possibly note how even the comparison of cinema usage notes a feeling amoung the civilians themselves - rom-coms and other escapist mediums seeing increased popularity by the end of the war, () noting implications of war weariness and a need to escape the brutality of everyday.
Interestingly however, while rom-coms gained increased prominence by the end of the war, movies encouraging debate on a new social order post-war were welcomed too. This was in great contrast to the German cinema experience, which saw Nazi ideology cleverly intertwined in film. Films such as () prompted.
Thus, analysis of the cinema provides an interesting section of home-front experience. A significantly favoured form of entertainment, the cinema shows how many sought an hour or two of escapism in a comfy chair, such desires evidence of (blah).
-
In both countries, censorship was imposed, the dissemination of newswas manipulated, and propaganda was issued; on the whole, however, thiswas a break with peacetime practice for Britons but a continuation of it forGermans.
Quote for cinema's? While () as the land of (), Britain too utilised censorship and propaganda to ensure morale. Neverthless, like Germany, () British cinema was not (), with films often utilising () to present messages. As such, we could argue that British and German civilians on the home front experienced a similar sort of experience in the cinema, where comedies and () were appreciated and increasingly made. Nevertheless, while Britain imposed newsreels within cinema, Germans saw themselves with (by blah) over 40 mins of news, something that the British did not face.
-
-
viewer.athenadocs.nl viewer.athenadocs.nl
-
Overig internationaal recht
recht dat is afgeleid van verdragen, dit zijn dus de regels die instelling en organen van de europese unie zelf creëren → verordeningen,richtlijnen, besluiten,aanbevelingen en besluiten
-
-
news.ycombinator.com news.ycombinator.com
-
What I'd really like to see is some kind of iframe that pins JS/wasm code within it to a particular bundle hash and prevents modification at runtime (even from chrome extensions).Something more like a TEE inside the browser of sorts.
So you want people to let you run code on their machine that makes it answer to you—some random nobody—instead of the person who is using, and very likely owns and paid for, the device in question.
Perhaps you would next like to see your neighbor to just give you their car and convince some local businesses to let you take over their employees, shops, cash registers, and other equipment to put them work for you as well.
-
-
www.americanyawp.com www.americanyawp.com
-
and I am glad that the omniscient God held the balance of battle in His Almighty hand, and that human slavery was swept forever from American soil — that the American Union was saved from the wreck of war.
yes slavery was erased from America and probability of it returning back is because of a smarter generation and
-
There was a South of slavery and secession — that South is dead. There is a South of union and freedom — that South, thank God, is living, breathing, growing every hour.
yes that south is had die, but that south created some of the worst conditions for blacks in america by developing the white supremacy thoughts
-
-
chem.libretexts.org chem.libretexts.org
-
Practice
on question 2 how do these numbers relate to the well.I understand the repulsion between nuclei and the attraction of electrons and nuclei and how this relates to equilibrium, but I do not understand how the numbers relate back to the model
-
-
www.theguardian.com www.theguardian.com
-
[[Cory Doctorow p]] on AI en the economic dynamic behind the hype that bigtech is pursuing to remain growth stocks even as monopolists. 'tech centaur' me in a car, a human head on something else vs 'reverse centaur' a meat puppet doing the machines bidding, e.g. an Amazon delivery driver
-
-
shs-cairn-info.bibelec.univ-lyon2.fr shs-cairn-info.bibelec.univ-lyon2.fr
-
la Troisième République – au moins jusqu’en 1914 – s’est toujours pensée sous le signe de la fragilité et du combat
=> trope de la "République en danger"
-
-
-
Keeping, onze urenregistratie maakt gebruik van DigitalOcean in een Amsterdams datacentrum voor de urenregistratie.
-
-
viewer.athenadocs.nl viewer.athenadocs.nl
-
agency relationship
Type 1: Shareholders hire managers or the board (Agents) to run for them. Conflict arises if these Agents prioritize their own interest. Type 2: Conflict between shareholders. Few dominant shareholders making decisions for benefit, harming minority shareholders
-
Two-tier board
A executive board and a board of supervisors
-
Foreign trade policy
Trade barriers and import controls
-
Exchange rate policy
Improving country trade competitiveness, fixed/floating exchange rates.
-
Monetary policy
Interest rates and money supply
-
Fiscal policy
Government spending and taxes
-
Auction markets
Has a physical location and primary purpose is to match the willing to sell with those buying.
-
Dealer markets
In Equities and long-term debts = Over-the-counter (OTC) markets)
-
Secondary markets
Markets, where the securities are bought and sold after original sale (Stock market)
-
-
github.com github.com
-
Commits on May 13, 2025docs(readme): add peersuitejeremyckahnauthored

-
-
-
Dutch ABP (a 500 billion pensionfund) dropped a third of their US treasury bills, 10 billion of 29 billion (March '25) to now 19 billion (Sept '25). The money was reinvested in Dutch and German bonds.
-
-
-
EU MS have agreed a ban on Russian LNG imports, Slovakia and Hungary against. Last yr the EP already agreed this ban. A proposal to ban oil imports from Russia is expected soon.
-
-
chem.libretexts.org chem.libretexts.org
-
Intermolecular Force" is a misnomer, even though it is commonly used, as these are the forces between ions with molecules possessing a dipole moment, and ions do not have to be molecular
Do molecules always have to be multiple ions/atoms? Can a single atom ever be considered a molecule?
-
Figure 11.2.1
What is the significance of the double ended arrow and the n above figure 11.2.1?
-
-
yandex.yandex.ru yandex.yandex.ru
-
PayBox
paybox.money?
-
Нам нужны бэкенд-разработчики.
0 беков?
-
-
-
eLife Assessment
This study presented valuable findings regarding the basic molecular pathways leading to the cystogenesis of Autosomal Dominant Polycystic Kidney Disease, suggesting BICC1 functions as both a minor causative gene for PKD and a modifier of PKD severity. Solid data were supplied to demonstrate the functional and structural interactions between BICC-1, PC1 and PC2, respectively. The characterization of such interactions remains to be developed further, which renders the specific relevance of these findings for the etiology of relevant diseases unclear.
-
Reviewer #1 (Public review):
In this manuscript, Tran et al. investigate the interaction between BICC1 and ADPKD genes in renal cystogenesis. Using biochemical approaches, they reveal a physical association between Bicc1 and PC1 or PC2 and identify the motifs in each protein required for binding. Through genetic analyses, they demonstrate that Bicc1 inactivation synergizes with Pkd1 or Pkd2 inactivation to exacerbate PKD-associated phenotypes in Xenopus embryos and potentially in mouse models. Furthermore, by analyzing a large cohort of PKD patients, the authors identify compound BICC1 variants alongside PKD1 or PKD2 variants in trans, as well as homozygous BICC1 variants in patients with early-onset and severe disease presentation. They also show that these BICC1 variants repress PC2 expression in cultured cells.
Overall, the concept that BICC1 variants modify PKD severity is plausible, the data are robust, and the conclusions are largely supported.
Comments on revision:
My comments have been mostly addressed.
-
Reviewer #2 (Public review):
Tran and colleagues report evidence supporting the expected yet undemonstrated interaction between the Pkd1 and Pkd2 gene products Pc1 and Pc2 and the Bicc1 protein in vitro, in mice, and collaterally, in Xenopus and HEK293T cells. The authors go on to convincingly identify two large and non-overlapping regions of the Bicc1 protein important for each interaction and to perform gene dosage experiments in mice that suggest that Bicc1 loss of function may compound with Pkd1 and Pkd2 decreased function, resulting in PKD-like renal phenotypes of different severity. These results led to examining a cohort of very early onset PKD patients to find three instances of co-existing mutations in PKD1 (or PKD2) and BICC1. Finally, preliminary transcriptomics of edited lines gave variable and subtle differences that align with the theme that Bicc1 may contribute to the PKD defects, yet are mechanistically inconclusive.
These results are potentially interesting, despite the limitation, also recognized by the authors, that BICC1 mutations seem exceedingly rare in PKD patients and may not "significantly contribute to the mutational load in ADPKD or ARPKD". The manuscript has several intrinsic limitations that must be addressed.
The manuscript contains factual errors, imprecisions, and language ambiguities. This has the effect of making this reviewer wonder how thorough the research reported and analyses have been.
Comments on revision:
My comments have been addressed.
-
Reviewer #3 (Public review):
Summary:
This study investigates the role of BICC1 in the regulation of PKD1 and PKD2 and its impact on cytogenesis in ADPKD. By utilizing co-IP and functional assays, the authors demonstrate physical, functional, and regulatory interactions between these three proteins.
Strengths:
(1) The scientific principles and methodology adopted in this study are excellent, logical, and reveal important insights into the molecular basis of cystogenesis.
(2) The functional studies in animal models provide tantalizing data that may lead to a further understanding and may consequently lead to the ultimate goal of finding a molecular therapy for this incurable condition.
(3) In describing the patients from the Arab cohort, the authors have provided excellent human data for further investigation in large ADPKD cohorts. Even though there was no patient material available, such as HUREC, the authors have studied the effects of BICC1 mutations and demonstrated its functional importance in a Xenopus model.
Weaknesses:
This is a well-conducted study and could have been even more impactful if primary patient material was available to the authors. A further study in HUREC cells investigating the critical regulatory role of BICC1 and potential interaction with mir-17 may yet lead to a modifiable therapeutic target.
Conclusion:<br /> The authors achieve their aims. The results reliably demonstrate the physical and functional interaction between BICC1 and PKD1/PKD2 genes and their products.
The impact is hopefully going to be manifold:
(1) Progressing the understanding of the regulation of the expression of PKD1/PKD2 genes.
Comments on revision:
My comments have been addressed and sorted.
-
Author response:
The following is the authors’ response to the original reviews.
Reviewer #1 (Public review):
(1) The authors devote significant effort to characterizing the physical interaction between Bicc1 and Pkd2. However, the study does not examine or discuss how this interaction relates to Bicc1's well-established role in posttranscriptional regulation of Pkd2 mRNA stability and translation efficiency.
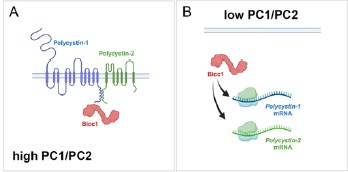
The reviewer is correct that the present study has not addressed the downstream consequences of uthis interaction considering that Bicc1 is a posttranscriptional regulator of Pkd2 (and potentially Pkd1). We think that the complex of Bicc1/Pkd1/Pkd2 retains Bicc1 in the cytoplasm and thus restrict its activity in participating in posttranscriptional regulation (see Author response image 1). We, however, do not yet have data to support this and thus have not included this model in the manuscript. Yet, we have updated the discussion of the manuscript to further elaborate on the potential mechanism of the Bicc1/Pkd1/Pkd2 complex.
We have updated the discussion to include a discussion on the potential consequences on posttranscriptional regulation by Bicc1.
Author response image 1.
Model of BICC1, PC1 and PC2 self-regulation. In this model Bicc1 acts as a positive regulator of PKD gene expression. In the presence of ‘sufficient’ amounts of PC1/PC2 complex, it is tethered to the complex and remains biologically inactive (Fig. 1A). However, once the levels of the PC1/PC2 complex are reduced, Bicc1 is now present in the cytoplasm to promote expression of the PKD proteins, thereby raising their levels (Fig. 4B), which then in turn will ‘shutdown’ Bicc1 activity by again tethering it to the plasma membrane.
(2) Bicc1 inactivation appears to downregulate Pkd1 expression, yet it remains unclear whether Bicc1 regulates Pkd1 through direct interaction or by antagonizing miR-17, as observed in Pkd2 regulation. This should be further examined or discussed.
This is a very interesting comment. Vishal Patel published that PKD1 is regulated by a mir-17 binding site in its 3’UTR (PMID: 35965273). We, however, have not evaluated whether BICC1 participates in this regulation. A definitive answer would require utilization of the mice described in above reference, which is beyond the scope of this manuscript. We, however, have revised the discussion to elaborate on this potential mechanism.
We have updated the discussion to include a statement on the potential direct regulation of Pkd1 mRNA by Bicc1.
(3) The evidence supporting Bicc1 and ADPKD gene cooperativity, particularly with Pkd1, in mouse models is not entirely convincing, likely due to substantial variability and the aggressive nature of Bpk/Bpk mice. Increasing the number of animals or using a milder Bicc1 strain, such as jcpk heterozygotes, could help substantiate the genetic interaction.
We have initially performed the analysis using our Bicc1 complete knockout, we previously reported on (PMID 20215348) focusing on compound heterozygotes. Yet, similar to the Pkd1/Pkd2 compound heterozygotes (PMID 12140187) no cyst development was observed when we sacrificed the mice as late as P21. Our strain is similar to the above mentioned jcpk, which is characterized by a short, abnormal transcript thought to result in a null allele (PMID: 12682776). We thank the reviewer for pointing us to the reference showing the heterozygous mice exhibit glomerular cysts in the adults (PMID: 7723240). This suggestion is an interesting idea we will investigate. In general, we agree with the reviewer that a better understanding of the contribution of Bicc1 to the adult PKD phenotype will be critical. To this end, we are currently generating a floxed allele of Bicc1 that will allow us to address the cooperativity in the adult kidney, when e.g. crossed to the Pkd1<sup>RC/RC</sup> mice. Yet, these experiments are beyond the timeframe for this revision.
No changes were made in the revised manuscript.
Reviewer #2 (Public review):
(1) These results are potentially interesting, despite the limitation, also recognized by the authors, that BICC1 mutations seem exceedingly rare in PKD patients and may not "significantly contribute to the mutational load in ADPKD or ARPKD". The manuscript has several intrinsic limitations that must be addressed.
As mentioned above, the study was designed to explore whether there is an interaction between BICC1 and the PKD1/PKD2 and whether this interaction is functionally important. How this translates into the clinical relevance will require additional studies (and we have addressed this in the discussion of the manuscript).
(2) The manuscript contains factual errors, imprecisions, and language ambiguities. This has the effect of making this reviewer wonder how thorough the research reported and analyses have been.
We respectfully disagree with the reviewer on the latter interpretation. The study was performed with rigor. We have carefully assessed the critiques raised by the reviewer. As presented below, most of the criticisms raised by the reviewer have been easily addressed in the revised version of the manuscript. Yet, none of the critiques seems to directly impact the overall interpretation of the data.
Reviewer #1 (Recommendations for the authors):
(1) The manuscript requires further editing. For example, figure panels and legends are mismatched in Figure 1
We have corrected the labeling of Figure 1.
(2) Y-axis units and values are inconsistent in Figures 4b-4g, Supplementary Figures S2e and S2f are not referenced in the text, genotypes are missing in Supplementary Figure S3f, and numerous typographical errors are present.
In respect to the y-axis in Figure 4b-g, the scale is different for each of them, but that is intentional as one would lose the differences if they were all scaled identically. But we have now mentioned this in the figure legend to make the reader aware of it. In respect to the Supplemental Figure S2e,f, we included the panels in the description of the mutant BICC1 lines, but unfortunately forgot to reference them. This has now been done.
We have updated the labeling of the Y-axis for the cystic indices adding “[%]” as the unit and updated the figure legend of Figure 4. We have included the genotypes in Supplementary Figure S3f. The Supplementary Figure S2e,f is now mentioned in the supplemental material (page 9, 2<sup>nd</sup> paragraph).
Reviewer #2 (Recommendations for the authors):
(1) Previous data from mouse, Xenopus, and zebrafish suggest a crucial role for the RNAbinding protein Bicc1 in the pathogenesis of PKD, although BICC1 mutations in human PKD have not been previously reported." The cited sources (and others that were not cited) link Bicc1 mutations to renal cysts, similar to a report by Kraus (PMID: 21922595) that the authors cite later. However, a more direct link to PKD was reported by Lian and colleagues using whole Pkd1 mice (PMID: 20219263) and by Gamberi and colleagues using Pkd1 kidneys and human microarrays (PMID: 28406902). Although relevant, neither is cited here, and only the former is cited later in the manuscript.
Thanks for pointing this out. We have added these three citations.
We have added these three citations (PMID: 21922595, PMID: 20219263 and PMID: 28406902) in the indicated sentence.
(2) In Figure 1B, the lanes do not seem to correspond among panels, particularly evident in the panel with myc-mBicc1. Hence, it is difficult to agree with the presented conclusions.
We have corrected the labeling of the lanes in Figure 1b.
(3) In the Figure 1 legend: "(g) Western blot analysis following co-IP experiments, using an anti-mouse Bicc1 or anti-goat PC2 antibody as bait, identified protein interactions between endogenous PC2 and BICC1 in UCL93 cells. Non-immune goat and mouse IgG were included as a negative control." There is no mention of panel H, although this reviewer can imagine what the authors meant. The capitalization differs in the figure and legend. More troublingly, in panel G, a non-defined star indicates a strong band present in both immune and non-immune control.
We have corrected the figure legend of Figure 1 and clarified the non-specific band in the figure legend.
(4) In Figure 4, the authors do not show the matched control for the Bicc1 Pkd1 interaction in panel d, nor do they show a scale bar in either a) or d). Thus, the phenotypic severity cannot be properly assessed.
Thanks for pointing out the missing scale bars, which have now been added. In respect to the two kidneys shown in Figure 4d, the two kidneys shown are from littermates to illustrate the kidney size in agreement with the cumulative data shown in Figure 4e. Unfortunately, this litter did not have a wildtype control. As the data analysis in Figure 4e is based on littermates, mixing and matching kidneys of different litters does not seem appropriate. Thus, we have omitted showing a wildtype control in this panel. However, the size of the wildtype kidney can be seen in Figure 4a.
We have added the scale bar to both panels and have updated the figure legend to emphasize that the kidneys shown are from littermates and that no wildtype littermate was present in this litter.
(5) "Surprisingly, an 8-fold stronger interaction was observed between full-length PC1 and myc-mBicc1-ΔKH compared to mycmBicc1 or myc-mBicc1-ΔSAM." Assuming all the controls for protein folding and expression levels have been carried out and not shown/mentioned, this sentence seems to contradict the previous statement that Bicc1deltaSAM reduced the interaction with PC1 by 55%. Because the full length and SAM deletion have different interaction strengths, the latter sentence makes no sense.
The reduction in the levels of myc-mBicc1-ΔSAM compared to wildtype mycmBicc1 in respect to PC1 binding was not significant. We have clarified this in the text.
We have corrected the sentence and modified the Figure accordingly.
(6) Imprecise statements make a reader wonder how to interpret the data: "More than three independent experiments were analyzed." Stating the sample size or including it in the figure would save space and improve confidence in the data presented.
We have stated the exact number of animals per conditions above each of the bars.
(7) "Next, we performed a similar mouse study for Pkd1 by reducing the gene dose of Pkd1 postnatally in the collecting ducts using a Pkhd1-Cre as previously described40" What did the authors mean?
The reference was included to cite the mouse strain, but realized that it can be mis-interpreted that the exact experiments has been performed previously. We have clarified this in the text.
We have reworded the sentence to avoid misinterpretation.
(8) The authors examined the additive effects of knocking down Bicc1, Pkd1, and Pkd2 with morpholinos in Xenopus and, genetically, in mice. While the Bicc1[+/-] Pkd1 or 2[+/-] double heterozygote mice did not show phenotypes, the authors report that the Bicc1[-/-] Pkd1 or 2 [+/-] did instead show enlarged kidneys. What is the phenotype of a Bicc1[+/-] Pkd1 or 2 [-/-]? What we learn from the author's findings among the PKD population suggests that the latter situation would be potentially translationally relevant.
The mouse experiments were designed to address a cooperativity between Bicc1 and either Pkd1 or Pkd2 and whether removal of one copy of Pkd1 or Pkd2 would further worsen the Bicc1 cystic kidney phenotype. Thus, the parental crosses were chosen to maximize the number of animals obtained for these genotypes. Unfortunately, these crosses did not yield the genotypes requested by the reviewer. To address the contribution of Bicc1 towards the PKD population, we will need to perform a different cross, where we eliminate Pkd1 or Pkd2 in a floxed background of Bicc1 postnatally in adult mice. While we are gearing up to perform such an experiment, this is timewise beyond the scope of the manuscript. In addition, please note that we have addressed the question about the translation towards the PKD population already in the discussion of the original submission (page 13/14, last/first paragraph).
No changes have been made to the revised version of the manuscript.
(9) How do the authors interpret the milder effects of the Bicc1[-/-] Pkd1[+/-] compared to Bicc1[-/-] Pkd2[+/-] relative to the respective protein-protein interactions?
The milder effects are due to the nature of the crosses. While the Pkd2 mutant is a germline mutation, the Pkd1 mutant is a conditional allele eliminating Pkd1 only in the collecting ducts of the kidney. As such, we spare other nephron segments such as the proximal tubules, which also significantly contribute to the cyst load. As such these mouse data support the interaction between Pkd1 and Pkd2 with Bicc1, but do not allow us to directly compare the outcomes. While this was mentioned in the previous version of the manuscript, we have expanded on this in the revised version of the manuscript.
We have expanded the results section in the revised version of the manuscript highlighting that the two different approaches cannot be directly compared.
(10) How do the authors interpret that the strong Bicc1[Bpk] Pkd1 or Pkd2 double heterozygote mice did not have defects and "kidneys from Bicc1+/-:Pkd2+/- did not exhibit cysts (data not shown)", when the VEO PKD patients and - although not a genetic reduction - also the morpholino-treated Xenopus did?
VEO PKD patients are characterized by a loss of function of PKD1 or PKD2 and – as we propose in this manuscript - that BICC1 further aggravates the phenotype. Yet, we do not address either in the mouse or Xenopus experiments whether BICC1 is a genetic modifier. We are simply addressing whether the two genes show a genetic interaction. In the mouse studies, we eliminate one copy of Pkd1 or Pkd2 in the background of a hypomorphic allele of Bicc1. Similarly, in the Xenopus experiments, we employ suboptimal doses of the morpholino oligomers, i.e., concentrations that did not yield a phenotypic change and then asked whether removing both together show cooperativity. It is important to state that this is based on a biological readout and not defined based on the amount of protein. While we have described this already in the original manuscript (page 7, first paragraph), we have amended our description of the Xenopus experiment to make this even clearer.
Finally, we agree with the reviewer that if we were to address whether Bicc1 is a modifier of the PKD phenotype in mouse, we would need to reduce Bicc1 function in a Pkd1 or Pkd2 mutants. Yet, we have recognized this already in the initial version of the manuscript in the discussion (page 14, first paragraph).
We have expanded the results section when discussing the suboptimal amounts of the morpholino oligos (Page 6, 1<sup>st</sup> paragraph).
(11) Unclear: "While variants in BICC1 are very rare, we could identify two patients with BICC1 variants harboring an additional PKD2 or PKD1 variant in trans, respectively." Shortly after, the authors state in apparent contradiction that "the patients had no other variants in any of other PKD genes or genes which phenocopy PKD including PKD1, PKD2, PKHD1, HNF1s, GANAB, IFT140, DZIP1L, CYS1, DNAJB11, ALG5, ALG8, ALG9, LRP5, NEK8, OFD1, or PMM2."
The reviewer is correct. This should have been phrased differently. We have now added “Besides the variants reported below” to clarify this more adequately.
The sentence was changed to start with “Besides the variants reported below, […].”
(12) "The demonstrated interaction of BICC1, PC1, and PC2 now provides a molecular mechanism that can explain some of the phenotypic variability in these families." How do the authors reconcile this statement with their reported ultra-rare occurrence of the BICC1 mutations?
As mentioned in the manuscript and also in response to the other two reviewers, Bicc1 has been shown to regulate Pkd2 gene expression in mice and frogs via an interaction with the miR-17 family of microRNAs. Moreover, the miR-17 family has been demonstrated to be critical in PKD (PMID: 30760828, PMID: 35965273, PMID: 31515477, PMID: 30760828). In fact, both other reviewers have pointed out that we should stress this more since Bicc1 is part of this regulatory pathway. Future experiments are needed to address whether Bicc1 contributes to the variability in ADPKD onset/severity. Yet, this is beyond the scope of this study.
Based on the comments of the two other reviewers we have further addressed the Bicc1/miR-17 interaction.
(13) The manuscript should use correct genetic conventions of italicization and capitalization. This is an issue affecting the entire manuscript. Some exemplary instances are listed below.
(a) "We also demonstrate that Pkd1 and Pkd2 modifies the cystic phenotype in Bicc1 mice in a dose-dependent manner and that Bicc1 functionally interacts with Pkd1, Pkd2 and Pkhd1 in the pronephros of Xenopus embryos." Genes? Proteins?
The data presented in this section show that a hypomorphic allele of Bicc1 in mouse and a knockdown in Xenopus yields this. As both affect the proteins, the spelling should reflect the proteins.
No changes have been made in the revised manuscript.
(b) The sentence seems to use both the human and mouse genetic capitalization, although it refers to experiments in the mouse system “to define the Bicc1 interacting domains for PC2 (Fig. 2d,e). Full-length PC2 (PC2-HA) interacted with full-length myc-mBICC1.”
We agree with the review that stating the species of the molecules used is critical, we have adapted a spelling of Bicc1, where BICC1 is the human homologue, mBicc1 is the mouse homologue and xBicc1 the Xenopus one.
We have highlighted the species spelling in the methods section and labeled the species accordingly throughout the manuscript and figures.
(14) “Together these data supported our biochemical interaction data and demonstrated that BICC1 cooperated with PKD1 and PKD2.” Are the authors implying that these results in mice will translate to the human protein?
We agree that we have not formally shown that the same applies to the human proteins. Thus, we have changed the spelling accordingly.
We have revised the capitalization of the proteins.
(15) The text is often unclear, terse, or inconsistent.
(a) “These results suggested that the interaction between PC1 and Bicc1 involves the SAM but not the KH/KHL domains (or the first 132 amino acids of Bicc1). It also suggests that the N-terminus could have an inhibitory effect on PC1-BICC1 association.” How do the authors define the N-terminus? The first 132 aa? KH/KHL domains?
This was illustrated in the original Figure 2A. The DKH constructs lack the first 351 amino acids.
To make this more evident, we have specified this in the text as well.
(b) Similarly, the authors state below, "Unlike PC1, PC2 interacted with mycmBICC1ΔSAM, but not myc-mBICC1-ΔKH suggesting that PC2 binding is dependent on the N-terminal domains but not the SAM domain." It is unclear if the authors refer to the KH/KHL domains or others. Whatever the reference to the N-terminal region, it should also be consistent with the section above.
This is now specified in the text.
(c) Unclear: "We have previously demonstrated that Pkd2 levels are reduced in a complete Bicc1 null mice,22 performing qRT-PCR of P4 kidneys (i.e. before the onset of a strong cystic phenotype), revealed that Bicc1, Pkd1 and Pkd2 were statistically significantly down9 regulated (Fig. 4h-j)".
We have changed the text to clarify this.
(d) “Utilizing recombinant GST domains of PC1 and PC2, we demonstrated that BICC1 binds to both proteins in GST-pulldown assays (Fig. 1a, b)." GST-tagged domains? Fusions?
We have changed the text to clarify this.
(e) "To study the interaction between BICC1, PKD1 and PKD2 we combined biochemical approaches, knockout studies in mice and Xenopus, genetic engineered human kidney cells" > genetically engineered.
We have changed the text to clarify this.
(f) Capitalization (e.g., see Figure S3, ref. the Bpk allele) and annotation (e.g., Gly821Glu and G821E) are inconsistent.
We have homogenized the labeling of the capitalization and annotations throughout the manuscript.
(g) What do the authors mean by "homozygous evolutionarily well-conserved missense variant"?
We have changed this is the revised version of the manuscript.
Reviewer #3 (Public review/Recommendations to the authors):
(1) A further study in HUREC cells investigating the critical regulatory role of BICC1 and potential interaction with mir-17 may yet lead to a modifiable therapeutic target.
(2) This study should ideally include experiments in HUREC material obtained from patients/families with BICC1 mutations and studying its effects on the PKD1/2 complex in primary cell lines.
This is an excellent suggestion. We agree with the reviewer that it would have been interesting to analyze HUREC material from the affected patients. Unfortunately, besides DNA and the phenotypic analysis described in the manuscript neither human tissue nor primary patient-derived cells collected once the two patients with the BICC1 p.Ser240Pro variant passed away.
No changes to the revised manuscript have been made to address this point.
(3) Please remove repeated words in the following sentence in paragraph 2 of the introduction: "BICC1 encodes an evolutionarily conserved protein that is characterized by 3 K-homology (KH) and 2 KH-like (KHL) RNA-binding domains at the N-terminus and a SAM domain at the C-terminus, which are separated by a by a disordered intervening sequence (IVS).23-28".
This has been changed.
-
-
www.americanyawp.com www.americanyawp.com
-
All men are created free and equal.” Taught now to live and work for the common weal, and not for the maintenance of a royal family or an overbearing aristocracy, not for the continuance of a social system which ranks them beneath an arrogant class of drones, children of Russian and German serfs, of Irish evicted tenants, Scotch crofters, and other victims of feudal tyranny, are translated into republican Americans, and are made in one love for a country which provides equal rights and privileges for all her children
in that time of the 1800's man write that all men are created free and equal but don't do what they write when they practice seprated but not equal to the black of america
-
children of Irishmen, Germans, Italians, Spaniards, and Swedes, side by side with the native American, all to be fused into one, in language, in thought, in feeling, and in patriotism.
in 1885 it seems that Andrew Carnegie noted did not included the american blacks who help build this country with free labor .
-
-
Local file Local file
-
he domes-tic economy of Nazi Germany relied on 7.5 million forced laborers, whosecontribution allowed the Third Reich to limit the industrial mobilization ofGerman women.
SLAY good quote for talking about women's work
-
Taking 1936 as the base (100), retail prices reached only 113 in 1944. However,as Jeremy Noakes has pointed out, civilian consumption was a better indicatorof the “extent of the sacrifices made by the populations.” On this measure, thedifficulties of both Germany and Japan were apparent. Compared to prewarlevels, civilian consumption fell in these countries respectively by 24 and 31percent; by contrast, it fell by only 16 percent in Britain, and it rose by an equalpercentage in the United States.
Could be good statistical evidence
-
But their economic preparations were also a function ofattitudes toward war in the interwar period itself. For this reason preparationswere extensive in Germany, much less so in the United Kingdom, and almostnonexistent in the United States.
However, such differences in initial female employment numbers and the voluntary beginings of womens work may be due to, Purseigle notes, Germany's position as aggressor, German women working in higher numbers due to mobilising earlier
-
ecause the out-come on the battlefield depended on the productive apparatus of the homefront.
good quote was home front different when gb was inning and germany was loosing?
-
, the relations between urban dwellers and rural populations exacer-bated these tensions as soon as access to foodstuffs became problemati
Interesting - could be something to look at with women maybe? Could look at how urban and rural women often were at odds with one another - arts seen as 'tarts' and evacuee women seen as feral in britain, was it the same in germany?
-
Aswomen’s contributions to the war effort challenged conventional gendereddefinitions of patriotic service, the demands of mobilization bore heavily on allsections of society.2
How did this demand be similar and different in each
-
-
juancarloscastillo.github.io juancarloscastillo.github.io
-
hallazgos
¿presentación de resultados o hallazgos?
-
repositorio reproducible
poner aquí (documentos dinámicos y reproducibles (R Markdown/Quarto), así se puede sacar el punto 6
-
-
-
peer to peer open construct workspace

-
-
bookshelf.vitalsource.com bookshelf.vitalsource.com
-
Increased travel.
I can relate to this as I wokr at planet fitness and live on the other side of the state so when I travel back with a certain illness, it can spread to another place. (on a small scale)
-
epidemiological transition, Omran (1971) divided the mortality experience of humankind into three stages—the Age of Pestilence and Famine, the Age of Receding Pandemics, and the Age of Degenerative and Human-Made Diseases.
Is this touching on how health problems are about llongterm life style factors?
-
-
www.engagingcommunities.org www.engagingcommunities.org
-
n the case of an ethnographic research project, primary research will take place at a specific research site, one of your own choosing
key component
-
Have you ever designed and/or administered a survey? These sorts of actions are categorized as primary research, research that involves direct collection of data from real world interactions.
These are important to keep in mind as it says these are categorized as primary research
-
-
social-media-ethics-automation.github.io social-media-ethics-automation.github.io
-
Authenticity is a concept we use to talk about connections and interactions when the way the connection is presented matches the reality of how it functions.
This definition elevates authenticity from "whether the content is true" to "whether the relationship is aligned": the type of interaction presented (friendly sharing, intimate confidences, genuine vulnerability) must be consistent with how it actually operates. In other words, authenticity is a kind of "contractual consistency"—what I think I'm getting is what I actually get. If an account uses "friend-like candor" to build intimacy, but is essentially just a marketing script run by a team, the problem isn't necessarily that it's a performance, but that it fails to make it clear to the audience what kind of relationship they are in, thus creating a gap between expectations and reality, and a feeling of being exploited. This also explains why some "performative" content (comedy accounts, role-playing) doesn't receive criticism: because its presentation and actual operation are consistent, and the audience knows what they are participating in.
-
As a rule, humans do not like to be duped.
This statement shifts the issue of "authenticity" from a moral judgment (you lied to me = you are bad) to a social mechanism (being deceived = a failure of the signaling system). In social interactions, people rely on various cues to determine who and what is trustworthy. When they discover they have been "manipulated" into believing something they shouldn't, they experience intense unease and anger, because this is not just a simple information error, but a threat to their judgment and sense of security. Cases like lonelygirl15 provoke a backlash not simply because the story is fake, but because the audience believed they were establishing a "real, intimate connection," only to discover that the connection had been disguised as something else from the very beginning.
-
Many users were upset that what they had been watching wasn’t authentic. That is, users believed the channel was presenting itself as true events about a real girl, and it wasn’t that at all. Though, even after users discovered it was fictional, the channel continued to grow in popularity.
Authenticity is what helps build trust between the poster and the audience. There isn't really any other way to do this other than maybe transparency but both tie together (I would argue). When you destroy that image that people had believed or built about you, it feels like a lie or deception which are not good associations to have.
-
In this section, it is clearly explained why authenticity is important and its relationship to trust and emotions. What caught my attention is the fact that being “duped” is not simply being wrong; it is also a sense of being manipulated. This is why people react very negatively to things they consider as “fake” on the web.
-
-
-
Nu.nl item saying the EC is seeking a court ordered ban on Grok in the EU. This was not mentioned in the EC press release on the extension of DSA investigations
-
-
ec.europa.eu ec.europa.eu
-
If proven, these failures would constitute infringements of Articles 34(1) and (2), 35(1) and 42(2) of the DSA.
The investigation concerns Article 34(1) and 34(2), 35(1) and 42(2).
-
he Commission has extended its ongoing formal proceedings opened against X in December 2023 to establish whether X has properly assessed and mitigated all systemic risks, as defined in the DSA, associated with its recommender systems, including the impact of its recently announced switch to a Grok-based recommender system.
The existing investigation of X under the DSA wrt recommender systems is extended in scope to include the recommender functions that Grok is announced to provide
-
The new investigation will assess whether the company properly assessed and mitigated risks associated with the deployment of Grok's functionalities into X in the EU. This includes risks related to the dissemination of illegal content in the EU, such as manipulated sexually explicit images, including content that may amount to child sexual abuse material.
A new investigation under the DSA wrt Grok and the production/dissemination of illegal incl sexualised imagery and CSAM
-
EC press release wrt investigations into X and Grok under the DSA.
-
-
viewer.athenadocs.nl viewer.athenadocs.nl
-
A second limitation of materialism is that nobody has a convincing idea of how the human mind could be a by-product of the biological processes in the brain.
Attempts to simulate the human mind as a by-product of biological or mechanical processes were not successful (cybernetics), whereas computers of a completely different structure (running sequences of instructions on stored information) started to thrive.
-
-
social-media-ethics-automation.github.io social-media-ethics-automation.github.io
-
Since we have different personas and ways of behaving in different groups of people, what happens if different groups of people are observing you at the same time? For example, someone might not know how to behave if they were at a restaurant with their friends and they noticed that their parents were seated at the table next to them. This is phenomenon is called “context collapse.” On social media, context collapse is a common concern, since on a social networking site you might be connected to very different people (family, different groups of friends, co-workers, etc.). Additionally, something that was shared within one context (like a private message), might get reposted in another context (publicly posted elsewhere).
Context collapse is a phenomenon which has ruined many peoples careers as a result. The importance of being able to code-switch allows for more interpersonal connections and often better outcomes. When others take advantage of these things, it really breaks some rules I believe.
-
The way we present ourselves to others around us (our behavior, social role, etc.) is called our public persona. We also may change how we behave and speak depending on the situation or who we are around, which is called code-switching.
Code switching happens, at least to me, unconsciously and it allows me to maintain healthy interactions and connections with people around me. I find it interesting that humans can adopt these different characters of themselves, it adds depth to who people really are.
-
How do you notice yourself changing how you express yourself in different situations, particularly on social media? Do you feel like those changes or expressions are authentic to who you are, do they compromise your authenticity in some way?
Naturally, it’s impossible for anyone to truly capture their entire selves in a social media profile. Everything is some type of performance to a certain degree, whether that’s informed by social media trends and behaviors or digital interactions.
-
-
moodle.u-bordeaux.fr moodle.u-bordeaux.fr
-
Abstract
Test 1-2 Test
-
-
www.euronews.com www.euronews.com
-
EC opens DSA investigation of X over Grok
-
-
www.youtube.com www.youtube.com
-
L'Intelligence Artificielle en Éducation : Défis Pédagogiques et Enjeux Démocratiques
Synthèse de la Direction
L'émergence de l'intelligence artificielle générative (IAG) en éducation représente bien plus qu'une simple innovation technique ; elle constitue une rupture anthropologique majeure.
Si l'IA promet une efficacité accrue par l'individualisation radicale des apprentissages via le learning analytics, elle menace paradoxalement les fondements de l'école républicaine : la construction du commun, l'exercice du jugement critique et le désir d'apprendre.
Le défi actuel n'est pas d'interdire l'outil, déjà omniprésent, mais de développer une pédagogie de la vigilance. Celle-ci repose sur le principe de réversibilité — n'utiliser l'IA que pour ce que l'on sait déjà faire — et sur la réaffirmation du rôle irremplaçable de l'enseignant comme passeur de valeurs et médiateur du débat démocratique.
--------------------------------------------------------------------------------
1. Nature et Fonctionnement de l'Intelligence Artificielle Générative
L'IA générative, popularisée par des outils comme ChatGPT ou Mistral, repose sur des mécanismes statistiques précis qui définissent ses capacités et ses limites.
Mécanismes techniques
• Base de données : Une accumulation massive de données (750 000 fois la Bible pour ChatGPT), qui reste néanmoins limitée par rapport à l'ensemble de la production humaine.
• Calculateur d'occurrences statistiques : L'IA ne « pense » pas ; elle calcule le mot qui a statistiquement le plus de probabilités de suivre le précédent.
• Le "Transformer" : Un outil récent permettant de prendre en compte le contexte pour affiner la pertinence statistique.
• Température et fluctuation : Réglée généralement à 0,8, la « température » permet d'introduire une part de fluctuation pour rendre les textes moins rigides et plus proches d'une opinion moyenne (opinion modale).
• Lissage linguistique : Un traitement systématique qui produit des textes à la syntaxe et à l'orthographe parfaites, souvent corrigés manuellement en amont par des opérateurs humains.
Une externalisation de la mémoire
L'IA s'inscrit dans la lignée historique de l'externalisation de la mémoire humaine (écriture, imprimerie, moteurs de recherche).
Ce phénomène soulève un débat ancien, déjà identifié par Platon dans le Phèdre : l'outil apporte-t-il la science ou seulement sa « semblance » ?
Le risque souligné est celui d'une remémoration venant « du dehors » plutôt que « du dedans », affaiblissant l'exercice même de la pensée.
--------------------------------------------------------------------------------
2. La Rupture du Learning Analytics et la Fin de la Forme Scolaire
L'IA introduit une rupture radicale à travers le learning analytics, une technique d'analyse de données visant à modéliser les stratégies d'apprentissage individuelles.
| Concept | Description et Conséquences | | --- | --- | | Individualisation Totale | Analyse des comportements sur tablette pour créer un logiciel strictement adapté au rythme, aux handicaps et aux préférences de l'élève. | | Séparation Instruction/Socialisation | Proposition de certains théoriciens (ex: Paul Jorion) de dissocier la transmission (confiée aux machines le matin) de la socialisation (activités sportives/artistiques l'après-midi). | | Obsolescence de la Classe | La classe traditionnelle, jugée inefficace pour gérer l'hétérogénéité, est remplacée par un tutorat machine disponible 24h/24. | | Risque d'Enfermement | L'adaptation permanente à l'utilisateur empêche la découverte de l'altérité et le dépassement de ses propres limites. |
--------------------------------------------------------------------------------
3. Ambitions vs Réalités : Une Analyse Critique
Le document identifie un décalage structurel entre les prétentions de l'IA et la réalité de sa production.
• L'accès à la connaissance : Si l'IA offre une rapidité d'investigation fabuleuse, elle est tributaire de sa base de données (biais idéologiques, absence d'événements censurés, prédominance masculine des concepteurs).
• La synthèse rigoureuse : L'IA privilégie l'académisme à la rigueur.
Elle procède par énumérations (souvent en base 3 ou 10) et agrège des concepts qu'il conviendrait de distinguer (ex: confondre besoin, niveau et intérêt).
• L'interdisciplinarité : Elle offre une illusion de complexité, mais réduit souvent le réel à des lieux communs et au "déjà-dit".
• La décision "pertinente" : En médecine ou en droit, l'IA réduit la situation (complexe et humaine) au seul problème (technique et algorithmique).
--------------------------------------------------------------------------------
4. Impacts et Défis pour l'Éducation
L'intégration de l'IA dans le milieu éducatif impose une refonte des pratiques d'évaluation et de transmission.
La mutation de l'évaluation
Face à l'industrialisation de la fraude, l'école doit :
• Passer du paradigme de la conformité (une seule bonne réponse) à celui de l'originalité de pensée.
• Réévaluer l'importance de l'oralité et du débat en face à face.
• Valoriser la démarche d'enquête (comment l'élève a cherché) plutôt que le seul résultat final.
Le principe de réversibilité
L'éducation doit enseigner que l'IA ne peut être utilisée que pour accélérer des tâches que l'individu sait déjà accomplir manuellement.
Utiliser l'IA pour ce que l'on ne maîtrise pas (ex: résumer un texte sans en comprendre la structure) conduit à une « bêtise artificielle » et à une perte de jugement.
Du savoir au désir d'apprendre
L'IA « comble le désir de savoir mais tue le désir d'apprendre ».
En fournissant des réponses immédiates, elle tarit la curiosité.
Le rôle de l'enseignant devient alors d'être un promoteur d'interrogations plutôt qu'un simple distributeur d'informations.
--------------------------------------------------------------------------------
5. IA, Réseaux Sociaux et Menaces sur la Démocratie
Le document souligne le lien entre l'IA et les mécanismes addictifs des réseaux sociaux, structurés pour enfermer l'utilisateur.
• Le tournant de 2009 : L'introduction des algorithmes de profilage (Facebook, puis TikTok) a remplacé l'ordre chronologique par le ciblage publicitaire.
• L'effet "Tunnel" : Contrairement à l'éducateur qui « ouvre des fenêtres », les algorithmes enferment l'individu dans ce qu'il aime déjà, empêchant toute sérendipité (découverte fortuite).
• L'anthropomorphisme (Effet Elisa) : L'IA se fait passer pour une personne pour gagner la confiance de l'utilisateur.
Il est impératif d'utiliser l'infinitif (ex: "faire", "chercher") plutôt que l'impératif pour marquer la distance avec la machine.
--------------------------------------------------------------------------------
6. Conclusions et Impératifs Éthiques
L'IA ne peut délibérer ni porter de valeurs. Elle ignore la temporalité humaine et la dimension incarnée du savoir.
Recommandations pour l'avenir :
1. Réhabiliter la conversation argumentée : Seul l'humain peut sortir d'un désaccord par le haut, en prenant en compte les divergences sans humilier l'autre.
2. Dénoncer le "solutionnisme technologique" : Tout problème humain n'est pas réductible à une solution technique. L'éthique doit primer sur l'efficacité.
3. Résister à la "machinisation" : Citant Adorno, le document rappelle que la barbarie commence par l'obéissance mécanique aux règles.
L'éducation doit donner la force de douter et de dire « non » aux évidences suggérées par les algorithmes.
En somme, l'IA doit rester un outil supervisé. L'enjeu civilisationnel est de préserver ce que seul l'humain peut faire : habiter sa parole, éprouver de la curiosité et construire un destin commun à travers le débat.
-
-
human.libretexts.org human.libretexts.org
-
undocumented immigration on homicide, aggravated assault, robbery, burglary and larceny crime rates.
Here's where those who would argue in favor of deporting ALL immigrants - documented or undocumented - would point out that there were no statistics on undocumented immigrants committing sexual assault, especially against children. That was one of the biggest rallying cries during both of the current president's election campaigns.
-
For example, we found in a 2017 study with colleagues that from 1970 to 2010 metropolitan areas with greater concentrations of immigrants, legal and undocumented combined, have less property crime than areas with fewer immigrants, on average. Critics suggested that our findings would not hold if we looked at only the subset of undocumented individuals.
From a purely scientific standpoint - and not just a racist xenophobic one - it's best to look at data from all viewpoints. In this case, it would be crime statistics from cities with greater concentrations of purely undocumented immigrants in one study, then in another, statistics from documented immigrants.Then, separate the statistics by race, ethnicity, gender, orientation, etc. - to see if their were any underlying causes for the crimes.
-
But undocumented immigrants, and immigrants more generally, are often baselessly blamed for increasing crime rates – including, repeatedly, by President Donald Trump. In the second and final presidential debate, Trump again claimed undocumented immigrants are rapists and murderers.
Why is this such a widespread belief? Is this another example of human's fear of the unknown being exploited for another human's personal gain?
-
-
stylo.ecrituresnumeriques.ca stylo.ecrituresnumeriques.cauntitled1
-
Titre 2
à renommer
-
-
shs-cairn-info.accesdistant.bu.univ-paris8.fr shs-cairn-info.accesdistant.bu.univ-paris8.fr
-
exprimées en cours d’activité, des interviews des personnels concernés et une analyse clinique des réactions et normes qui émergent au sein des collectifs de travail. La conclusion so
je ne suis pas d'accord avec cet exemple
-
-
social-media-ethics-automation.github.io social-media-ethics-automation.github.io
-
Separately, in 2018 during the MeToo movement, one of @Sciencing_Bi’s friends, Dr. BethAnn McLaughlin (a white woman), co-founded the MeTooSTEM non-profit organization, to gather stories of sexual harassment in STEM (Science, Technology, Engineering, Math). Kyle also followed her on Twitter until word later spread of Dr. McLaughlin’s toxic leadership and bullying in the MeTooSTEM organization (Kyle may have unfollowed @Sciencing_Bi at the same time for defending Dr. McLaughlin, but doesn’t remember clearly).
Authenticity is vital for maintaining public trust and the lack of it cause audiences to lose faith in the credibility of the information they receive from an individual or organization if they deem it inauthentic. However the norm is inauthenticity, where personas and identity are carefully crafted in order to boost engagement, this however is a very risky endeavor as it cause the groups that already agree with the perspective of the poster to stick around while those who value integrity and truthfulness to leave once they see the fakeness.
-
In 2016, the Twitter account @Sciencing_Bi was created by an anonymous bisexual Native American Anthropology professor at Arizona State University (ASU). She talked about her experiences of discrimination and about being one of the women who was sexually harassed by a particular Harvard professor. She gained a large Twitter following among academics, including one of the authors of this book, Kyle.
This is an example of how online authenticity is often tied to experience rather than physical identity. While @Sciencing_Bi was an anonymous identity, it was still an authentic identity to many academics in that it shared experiences of discrimination.
-
There are many ways inauthnticity shows up on internet-based social media, such as: Catfishing: Create a fake profile that doesn’t match the actual user, usually in an attempt to trick or scam someone Sockpuppet (or a “burner” account): Creating a fake profile in order to argue a position (sometimes intentionally argued poorly to make the position look bad)
I think inauthenticity is just an inevitable thing about social media if not a defining factor. Nowadays with so many bots rampant across different platforms, and AI generated, automated content (i.e. the Dead Internet Theory), social media has become characterized by fake stories and lies. Inauthenticity ranges from someone lying about an anecdote to full-blown fake news.
-
-
social-media-ethics-automation.github.io social-media-ethics-automation.github.io
-
Parasocial relationships are not a new phenomenon, but social media has increased our ability to form both sides of these bonds. As comedian Bo Burnham put it: “This awful D-list celebrity pressure I had experienced onstage has now been democratized.”
Parasocial relationship as a phenomenon has become quite widespread do to social media. I sure even without social media it would still have been prevalent, imagine a Queen or a president from the past who's life was well documented and shared to the public leading to many folk feeling as if they were closer to their leader. I wonder what negative effects this type of relationship could have even to a mild extent?
-
-
www.biorxiv.org www.biorxiv.org
-
Author response:
Reviewer #1 (Public review):
The authors analysed large-scale brain-state dynamics while humans watched a short video. They sought to identify the role of thalamocortical interactions.
Major concerns
(1) Rationale for using the naturalistic stimulus
In terms of brain state dynamics, previous studies have already reported large-scale neural dynamics by applying some data-driven analyses, like energy landscape analysis and Hidden Markov Model, to human fMRI/EEG data recorded during resting/task states. Considering such prior work, it'd be critical to provide sufficient biological rationales to perform a conceptually similar study in a naturalistic condition, i.e., not just "because no previous work has been done". The authors would have to clarify what type of neural mechanisms could be missed in conventional resting-state studies using, say, energy landscape analysis, but could be revealed in the naturalistic condition.
We appreciate your insightful comments regarding the need for a biological rationale in our study. As you mentioned, there are similar studies, just like Meer et al. utilized Hidden Markov Models to identify various activation modes of brain networks that included subcortical regions[1], Song et al. linked brain states to narrative understandings and attentional dynamics[2, 3]. These studies could answer why we use naturalistic stimuli datasets. Moreover, there is evidence suggesting that the thalamus plays a crucial role in processing information in a more naturalistic context while pointing out the vital role in thalamocortical communications[4, 5]. So, we tended to bridge thalamic activity and cortical state transition using the energy landscape description.
To address these gaps in conventional resting-state studies, we explored an alternative method—maximum entropy modeling based on the energy landscape. This allowed us to validate how the thalamus responds to cortical state transitions. To enhance clarity, we will update our introduction to emphasize the motivations behind our research and the significance of examining these neural mechanisms in a naturalistic setting.
(2) Effects of the uniqueness of the visual stimulus and reproducibility
One of the main drawbacks of the naturalistic condition is the unexpected effects of the stimuli. That is, this study looked into the data recorded from participants who were watching Sherlock, but what would happen to the results if we analyzed the brain activity data obtained from individuals who were watching different movies? To ensure the generalizability of the current findings, it would be necessary to demonstrate qualitative reproducibility of the current observations by analysing different datasets that employed different movie stimuli. In fact, it'd be possible to find such open datasets, like www.nature.com/articles/s41597-023-02458-8.
We appreciate your concern regarding the reproducibility of our findings. The dataset from the "Sherlock" study is of high quality and has shown good generalizability in various research contexts. We acknowledge the importance of validating our results with different datasets to enhance the robustness of our conclusions. While we are open to exploring additional datasets, we intend to pursue this validation once we identify a suitable alternative. Currently, we are considering a comparison with the dataset from "Forrest Gump" as part of our initial plan.
(3) Spatial accuracy of the "Thalamic circuit" definition
One of the main claims of this study heavily relies on the accuracy of the localization of two different thalamic architectures: matrix and core. Given the conventional or relatively low spatial resolution of the fMRI data acquisition (3x3x3 mm^3), it appears to be critically essential to demonstrate that the current analysis accurately distinguished fMRI signals between the matrix and core parts of the thalamus for each individual.
We acknowledge the importance of accurately localizing the different thalamic architectures, specifically the matrix and core regions. To address this, we downsampled the atlas of matrix and core cell populations from the previous study from a resolution of 2x2x2 mm<sup>3</sup> to 3x3x3 mm<sup>3</sup>, which aligns with our fMRI data acquisition. We would report the atlas as Supplementary Figures in our revision.
(4) More detailed analysis of the thalamic circuits
In addition, if such thalamic localisation is accurate enough, it would be greatly appreciated if the authors perform similar comparisons not only between the matrix and core architectures but also between different nuclei. For example, anterior, medial, and lateral groups (e.g., pulvinar group). Such an investigation would meet the expectations of readers who presume some microscopic circuit-level findings.
We appreciate your suggestion regarding a more detailed analysis of thalamic circuits. We have touched upon this in the discussion section as a forward-looking consideration. However, we believe that performing nuclei segmentation with 3T fMRI may not be ideal due to well-documented concerns regarding signal-to-noise ratio and spatial resolution. That said, we are interested in exploring these nuclei-pathway connections to cortical areas in future studies with a proper 7T fMRI naturalistic dataset.
(5) Rationale for different time window lengths
The authors adopted two different time window lengths to examine the neural dynamics. First, they used a 21-TR window for signal normalisation. Then, they narrowed down the window length to 13-TR periods for the following statistical evaluation. Such a seemingly arbitrary choice of the shorter time window might be misunderstood as a measure to relax the threshold for the correction of multiple comparisons. Therefore, it'd be appreciated if the authors stuck to the original 21-TR time window and performed statistical evaluations based on the setting.
Thank you for your valuable feedback regarding the choice of time window lengths. We aimed to maintain consistency in window lengths across our analyses. In light of your comments and suggestions from other reviewers, we plan to test our results using different time window lengths and report findings that generalize across these variations. Should the results differ significantly, we will discuss the implications of this variability in our revised manuscript.
(6) Temporal resolution
After identifying brain states with energy landscape analysis, this study investigated the brain state transitions by directly looking into the fMRI signal changes. This manner seems to implicitly assume that no significant state changes happen in one TR (=1.5sec), which needs sufficient validation. Otherwise, like previous studies, it'd be highly recommended to conduct different analyses (e.g., random-walk simulation) to address and circumvent this problem.
Thank you for raising this important point regarding temporal resolution. Many fMRI studies, such as those examining event boundaries during movie watching, operate under similar assumptions concerning state changes within one TR. For example, Barnett et al. processed the dynamic functional connectivity (dFC) with a window of 20 TRs (24.4s). So, we do not think it is a limitation but is a common question related to fMRI scanning parameters. To strengthen our analysis of state transitions and ensure they are not merely coincidental, we plan to conduct random-walk simulations, as suggested, to validate our findings in accordance with methodologies used in previous research.
Reviewer #2 (Public review):
Summary:
In this study, Liu et al. investigated cortical network dynamics during movie watching using an energy landscape analysis based on a maximum entropy model. They identified perception- and attention-oriented states as the dominant cortical states during movie watching and found that transitions between these states were associated with inter-subject synchronization of regional brain activity. They also showed that distinct thalamic compartments modulated distinct state transitions. They concluded that cortico-thalamo-cortical circuits are key regulators of cortical network dynamics.
Strengths:
A mechanistic understanding of cortical network dynamics is an important topic in both experimental and computational neuroscience, and this study represents a step forward in this direction by identifying key cortico-thalamo-cortical circuits. The analytical strategy employed in this study, particularly the LASSO-based analysis, is interesting and would be applicable to other data types, such as task- and resting-state fMRI.
We thanks for this comment and encouragement.
Weaknesses:
Due to issues related to data preprocessing, support for the conclusions remains incomplete. I also believe that a more careful interpretation of the "energy" derived from the maximum entropy model would greatly clarify what the analysis actually revealed.
Thank you for your valuable suggestions, and we apologize for any misunderstandings regarding the interpretation of the energy landscape in our study. To address this issue, we will include a dedicated paragraph in both the methods and results sections to clarify our use of the term "energy" derived from the maximum entropy model. This addition aims to eliminate any ambiguity and provide a clearer understanding of what our analysis reveals.
(1) I think the method used for binarization of BOLD activity is problematic in multiple ways.
a) Although the authors appear to avoid using global signal regression (page 4, lines 114-118), the proposed method effectively removes the global signal. According to the description on page 4, lines 117-122, the authors binarized network-wise ROI signals by comparing them with the cross-network BOLD signal (i.e., the global signal): at each time point, network-wise ROI signals above the cross-network signal were set to 1, and the rest were set to −1. If I understand the binarization procedure correctly, this approach forces the cross-network signal to be zero (up to some noise introduced by the binarization of network-wise signals), which is essentially equivalent to removing the global signal. Please clarify what the authors meant by stating that "this approach maintained a diverse range of binarized cortical states in data where the global signal was preserved" (page 4, lines 121-122).
Thank you for highlighting the potential issue with our binarization method. We appreciate your insights regarding the comparison of network-wise ROI signals with the cross-network BOLD signal, as this may inadvertently remove the global signal. To address this, we will conduct a comparative analysis of results obtained from both our current approach and the original pipeline. If we decide to retain our current method, we will carefully reconsider the rationale and rephrase our descriptions to ensure clarity regarding the preservation of the global signal and the diversity of binarized cortical states.
b) The authors might argue that they maintained a diverse range of cortical states by performing the binarization at each time point (rather than within each network). However, I believe this introduces another problem, because binarizing network-wise signals at each time point distorts the distribution of cortical states. For example, because the cross-network signal is effectively set to zero, the network cannot take certain states, such as all +1 or all −1. Similarly, this binarization biases the system toward states with similar numbers of +1s and −1s, rather than toward unbalanced states such as (+1, −1, −1, −1, −1, −1). These constraints and biases are not biological in origin but are simply artifacts of the binarization procedure. Importantly, the energy landscape and its derivatives (e.g., hard/easy transitions) are likely to be affected by these artifacts. I suggest that the authors try a more conventional binarization procedure (i.e., binarization within each network), which is more robust to such artifacts.
Related to this point, I have a question regarding Figure S1, in which the authors plotted predicted versus empirical state probabilities. As argued above, some empirical state probabilities should be zero because of the binarization procedure. However, in Figure S1, I do not see data points corresponding to these states (i.e., there should be points on the y-axis). Did the authors plot only a subset of states in Figure S1? I believe that all states should be included. The correlation coefficient between empirical and predicted probabilities (and the accuracy) should also be calculated using all states.
Thank you for your thoughtful examination of our data processing pipeline. We agree that a comparison between the conventional binarization method and our current approach is warranted, and we appreciate your suggestion. Upon reviewing Figure S1, we discovered that there was indeed an error related to the plotting style set to "log10." As you correctly pointed out, the data should reflect that the probabilities for states where all networks are either activated or deactivated are zero. We are very interested in exploring the state distributions obtained from both the original and current approaches, as your comments highlight important considerations. We sincerely appreciate your insightful feedback and will make sure to address these points thoroughly in our first revision.
c) The current binarization procedure likely inflates non-neuronal noise and obscures the relationship between the true BOLD signal and its binarized representation. For example, consider two ROIs (A and B): both (+2%, +1%) and (+0.01%, −0.01%) in BOLD signal changes would be mapped to (+1, −1) after binarization. This suggests that qualitatively different signal magnitudes are treated identically. I believe that this issue could be alleviated if the authors were to binarize the signal within each network, rather than at each time point.
Thank you for your important observation regarding the potential inflation of non-neuronal noise in our current binarization procedure. We recognize that this process could lead to qualitatively different signal magnitudes being treated similarly after binarization, as you illustrated with your example. While we acknowledge your point, we believe that conventional binarization pipelines may also encounter this issue, albeit by comparing signals to a network's temporal mean activity. To address this concern and maintain consistency with previous studies, we will discuss this limitation in our revised manuscript. Additionally, if deemed necessary, we will explore implementing a percentile-based threshold above the baseline to further refine our binarization approach. Your suggestion provides a valuable perspective, and we appreciate your insights.
(2) As the authors state (page 5, lines 145-148), the "energy" described in the energy landscape is not biological energy but rather a statistical transformation of probability distributions derived from the Boltzmann distribution. If this is the case, I believe that Figure 2A is potentially misleading and should be removed. This type of schematic may give the false impression that cortical state dynamics are governed by the energy landscape derived from the maximum entropy model (which is not validated).
Thank you for your valuable feedback regarding Figure 2A. We apologize for any confusion it may have created. While we recognize that similar figures are commonly used in literature involving energy landscapes (maximum entropy model), we agree that Figure 2A may mislead readers into thinking that cortical state dynamics are directly governed by the energy landscape derived from the maximum entropy model, which has not been validated. In light of your comments, we will remove Figure 2A and instead emphasize the analytical strategy presented in Figure 2B. Additionally, we will provide a simplified line graph as an illustrative example to clarify the concepts without the potential for misinterpretation.
Reviewer #3 (Public review):
Summary:
In this study, Liu et al. analyze fMRI data collected during movie watching, applied an energy landscape method with pairwise maximum entropy models. They identify a set of brain states defined at the level of canonical functional networks and quantify how the brain transitions between these states. Transitions are classified as "easy" or "hard" based on changes in the inferred energy landscape, and the authors relate transition probabilities to inter-subject correlation. A major emphasis of the work is the role of the thalamus, which shows transition-linked activity changes and dynamic connectivity patterns, including differential involvement of parvalbumin- and calbindin-associated thalamic subdivisions.
Strengths:
The study is methodologically complex and technically sophisticated. It integrates advanced analytical methods into high-dimensional fMRI data. The application of energy landscape analysis to movie-watching data appears to be novel as well. The finding on the thalamus involved energy state transition and provides a strong linkage to several theories on thalamic control functions, which is a notable strength.
Thanks for your comments on the novelty of our study.
Weaknesses:
The main weakness is the conceptual clarity and advances that this otherwise sophisticated set of analyses affords. A central conceptual ambiguity concerns the energy landscape framework itself. The authors note that the "energy" in this model is not biological energy but a statistical quantity derived from the Boltzmann distribution. After multiple reads, I still have major trouble mapping this measure onto any biological and cognitive operations. BOLD signal is a measure of oxygenation as a proxy of neural activity, and correlated BOLD (functional connectivity) is thought to measure the architecture of information communication of brain systems. The energy framework described in the current format is very difficult for most readers to map onto any neural or cognitive knowledge base on the structure and function of brain systems. Readers unfamiliar with maximum entropy models may easily misinterpret energy changes as reflecting metabolic cost, neural effort, or physiological variables, and it is just very unclear what that measure is supposed to reflect. The manuscript does not clearly articulate what conceptual and mechanistic advances the energy formalism provides beyond a mathematical and statistical report. In other words, beyond mathematical description, it is very hard for most readers to understand the process and function of what this framework is supposed to tell us in regards to functional connectivity, brain systems, and cognition. The brain is not a mathematical object; it is a biological organ with cognitive functions. The impact of this paper is severely limited until connections can be made.
Thank you for your insightful and constructive comments regarding the conceptual clarity of our energy landscape framework. We appreciate your perspective on the challenges of mapping the statistical measure of "energy" derived from the Boltzmann distribution onto biological and cognitive operations. To address these concerns, we will revise our manuscript to clarify our expressions surrounding "energy" and emphasize its probabilistic nature. Additionally, we will incorporate a series of analyses that explicitly relate the features of the energy landscape to cognitive processes and key parameters, such as brain integration and functional connectivity. We believe these changes will help bridge the gap between our mathematical framework and its relevance to understanding brain systems and cognitive functions.
Relatedly, the use of metaphors such as "valleys," "hills," and "routes" in multidimensional measures lacks grounding. Valleys and hills of what is not intuitive to understand. Based on my reading, these features correspond to local minima and barriers in a probability distribution over binarized network activation patterns, but similar to the first point, the manuscript does not clearly explain what it means conceptually, neurobiologically, or computationally for the brain to "move" through such a landscape. The brain is not computing these probabilities; they are measurement tools of "something". What is it? To advance beyond mathematical description, these measurements must be mapped onto neurobiological and cognitive information.
Thank you for your valuable feedback. In our revisions, we would aim to link the concept of rapid transition routes in the energy landscape to cognitive processes, such as narrative understanding and related features. By exploring these connections, we hope to provide a clearer context for how our framework can enhance understanding of cognitive functions and their neural correlates.
This conceptual ambiguity goes back to the Introduction. At the level of motivation, the purpose and deliverables of the study are not defined in the Introduction. The stated goal is "Transitions between distinct cortical brain states modulate the degree of shared neural processing under naturalistic conditions". I do not know if readers will have a clear answer to this question at the end. Is the claim that state transitions cause changes in inter-subject correlation, that they index moments of narrative alignment, or that they reflect changes in attentional or cognitive mode? This level of explanation is largely dissociated from the methods in their current form.
Thank you for highlighting this important point regarding the conceptual clarity in our Introduction. We appreciate your feedback about the motivation and objectives of the study. To clarify the stated goal of investigating how transitions between distinct cortical brain states modulate shared neural processing under naturalistic conditions, we will revise the manuscript to explicitly define the specific claims we aim to address. We will ensure that these explanations are closely tied to the methods employed in our study, providing a clearer framework for our readers.
Several methodological choices can use clarification. The use of a 21-TR window centered on transition offsets is unusually long relative to the temporal scale of fMRI dynamics and to the hypothesized rapidity of state transitions. On a related note, what is the temporal scale of state transition? Is it faster than 21 TRs?
Thank you for your insightful questions regarding our methodological choices. Our focus on specific state transitions necessitated the use of a 21-TR window. While it’s true that other transitions may occur within this window, averaging across the same transitions at different times allows us to identify distinctive thalamic BOLD patterns that precede cortical state transitions. This methodology enables us to capture relevant dynamics while ensuring that we focus on the transitions of interest. We appreciate your feedback, and this clarification will be included in our revised manuscript. We would also add a figure that describe the dwell time of cortical states.
The choice of movie-watching data is a strength. But, many of the analyses performed here, energy landscape estimation, clustering of states, could in principle be applied to resting-state data. The manuscript does not clearly articulate what is gained, mechanistically or cognitively, by using movie stimuli beyond the availability of inter-subject correlation.
Thank you for your question, which closely aligns with a concern raised by Reviewer #1. Our core hypothesis posits that naturalistic stimuli yield a broader set of brain states compared to those observed during resting-state conditions. To support this assertion, we will clearly articulate the findings from previous studies that relate to this hypothesis. Additionally, if appropriate, we will provide a comparative analysis between our data and resting-state data to highlight the differences and emphasize the uniqueness of the brain states elicited by naturalistic stimuli.
Because of the above issues, a broader concern throughout the results is the largely descriptive nature of the findings. For example, the LASSO analysis shows that certain state transitions predict ISC in a subset of regions, with respectable R² values. While statistically robust, the manuscript provides little beyond why these particular transitions should matter, what computations they might reflect, or how they relate to known cognitive operations during movie watching. Similar issues arise in the clustering analyses. Clustering high-dimensional fMRI-derived features will almost inevitably produce structure, whether during rest, task, or naturalistic viewing. What is missing is an explanation of why these specific clusters are meaningful in functional or mechanistic terms.
Thank you for your questions. In our revisions, we will perform additional analyses aimed at linking state transitions to cognitive processes more explicitly. Regarding clustering, we will provide a thorough discussion in the revised manuscript.
Finally, the treatment of the thalamus, while very exciting, could use a bit more anatomical and circuit-level specificity. The manuscript largely treats the thalamus as a unitary structure, despite decades of work demonstrating big functional and connectivity differences across thalamic nuclei. A whole-thalamus analysis without more detailed resolution is increasingly difficult to justify. The subsequent subdivision into PVALB- and CALB-associated regions partially addresses this, but these markers span multiple nuclei with overlapping projection patterns.
This suggestion aligns with the feedback from Reviewer #1. We believe that performing nuclei segmentation with 3T fMRI may not be ideal due to well-documented concerns regarding signal-to-noise ratio and spatial resolution. Therefore, investigating core and matrix cell projections across different thalamic nuclei using 7T fMRI presents a promising avenue for further study.
(1) Van Der Meer J N, Breakspear M, Chang L J, et al. Movie viewing elicits rich and reliable brain state dynamics [J]. Nature Communications, 2020, 11(1): 5004.
(2) Song H, Park B Y, Park H, et al. Cognitive and Neural State Dynamics of Narrative Comprehension [J]. Journal of Neuroscience, 2021, 41(43): 8972-8990.
(3) Song H, Shim W M, Rosenberg M D. Large-scale neural dynamics in a shared low-dimensional state space reflect cognitive and attentional dynamics [J]. Elife, 2023, 12.
(4) Shine J M, Lewis L D, Garrett D D, et al. The impact of the human thalamus on brain-wide information processing [J]. Nature Reviews Neuroscience, 2023, 24(7): 416-430.
(5) Yang M Y, Keller D, Dobolyi A, et al. The lateral thalamus: a bridge between multisensory processing and naturalistic behaviors [J]. Trends in Neurosciences, 2025, 48(1): 33-46.
-
Reviewer #3 (Public review):
Summary:
In this study, Liu et al. analyze fMRI data collected during movie watching, applied an energy landscape method with pairwise maximum entropy models. They identify a set of brain states defined at the level of canonical functional networks and quantify how the brain transitions between these states. Transitions are classified as "easy" or "hard" based on changes in the inferred energy landscape, and the authors relate transition probabilities to inter-subject correlation. A major emphasis of the work is the role of the thalamus, which shows transition-linked activity changes and dynamic connectivity patterns, including differential involvement of parvalbumin- and calbindin-associated thalamic subdivisions.
Strengths:
The study is methodologically complex and technically sophisticated. It integrates advanced analytical methods into high-dimensional fMRI data. The application of energy landscape analysis to movie-watching data appears to be novel as well. The finding on the thalamus involved energy state transition and provides a strong linkage to several theories on thalamic control functions, which is a notable strength.
Weaknesses:
The main weakness is the conceptual clarity and advances that this otherwise sophisticated set of analyses affords. A central conceptual ambiguity concerns the energy landscape framework itself. The authors note that the "energy" in this model is not biological energy but a statistical quantity derived from the Boltzmann distribution. After multiple reads, I still have major trouble mapping this measure onto any biological and cognitive operations. BOLD signal is a measure of oxygenation as a proxy of neural activity, and correlated BOLD (functional connectivity) is thought to measure the architecture of information communication of brain systems. The energy framework described in the current format is very difficult for most readers to map onto any neural or cognitive knowledge base on the structure and function of brain systems. Readers unfamiliar with maximum entropy models may easily misinterpret energy changes as reflecting metabolic cost, neural effort, or physiological variables, and it is just very unclear what that measure is supposed to reflect. The manuscript does not clearly articulate what conceptual and mechanistic advances the energy formalism provides beyond a mathematical and statistical report. In other words, beyond mathematical description, it is very hard for most readers to understand the process and function of what this framework is supposed to tell us in regards to functional connectivity, brain systems, and cognition. The brain is not a mathematical object; it is a biological organ with cognitive functions. The impact of this paper is severely limited until connections can be made.
Relatedly, the use of metaphors such as "valleys," "hills," and "routes" in multidimensional measures lacks grounding. Valleys and hills of what is not intuitive to understand. Based on my reading, these features correspond to local minima and barriers in a probability distribution over binarized network activation patterns, but similar to the first point, the manuscript does not clearly explain what it means conceptually, neurobiologically, or computationally for the brain to "move" through such a landscape. The brain is not computing these probabilities; they are measurement tools of "something". What is it? To advance beyond mathematical description, these measurements must be mapped onto neurobiological and cognitive information.
This conceptual ambiguity goes back to the Introduction. At the level of motivation, the purpose and deliverables of the study are not defined in the Introduction. The stated goal is "Transitions between distinct cortical brain states modulate the degree of shared neural processing under naturalistic conditions". I do not know if readers will have a clear answer to this question at the end. Is the claim that state transitions cause changes in inter-subject correlation, that they index moments of narrative alignment, or that they reflect changes in attentional or cognitive mode? This level of explanation is largely dissociated from the methods in their current form.
Several methodological choices can use clarification. The use of a 21-TR window centered on transition offsets is unusually long relative to the temporal scale of fMRI dynamics and to the hypothesized rapidity of state transitions. On a related note, what is the temporal scale of state transition? Is it faster than 21 TRs?
The choice of movie-watching data is a strength. But, many of the analyses performed here, energy landscape estimation, clustering of states, could in principle be applied to resting-state data. The manuscript does not clearly articulate what is gained, mechanistically or cognitively, by using movie stimuli beyond the availability of inter-subject correlation.
Because of the above issues, a broader concern throughout the results is the largely descriptive nature of the findings. For example, the LASSO analysis shows that certain state transitions predict ISC in a subset of regions, with respectable R² values. While statistically robust, the manuscript provides little beyond why these particular transitions should matter, what computations they might reflect, or how they relate to known cognitive operations during movie watching. Similar issues arise in the clustering analyses. Clustering high-dimensional fMRI-derived features will almost inevitably produce structure, whether during rest, task, or naturalistic viewing. What is missing is an explanation of why these specific clusters are meaningful in functional or mechanistic terms.
Finally, the treatment of the thalamus, while very exciting, could use a bit more anatomical and circuit-level specificity. The manuscript largely treats the thalamus as a unitary structure, despite decades of work demonstrating big functional and connectivity differences across thalamic nuclei. A whole-thalamus analysis without more detailed resolution is increasingly difficult to justify. The subsequent subdivision into PVALB- and CALB-associated regions partially addresses this, but these markers span multiple nuclei with overlapping projection patterns.
-
Reviewer #2 (Public review):
Summary:
In this study, Liu et al. investigated cortical network dynamics during movie watching using an energy landscape analysis based on a maximum entropy model. They identified perception- and attention-oriented states as the dominant cortical states during movie watching and found that transitions between these states were associated with inter-subject synchronization of regional brain activity. They also showed that distinct thalamic compartments modulated distinct state transitions. They concluded that cortico-thalamo-cortical circuits are key regulators of cortical network dynamics.
Strengths:
A mechanistic understanding of cortical network dynamics is an important topic in both experimental and computational neuroscience, and this study represents a step forward in this direction by identifying key cortico-thalamo-cortical circuits. The analytical strategy employed in this study, particularly the LASSO-based analysis, is interesting and would be applicable to other data types, such as task- and resting-state fMRI.
Weaknesses:
Due to issues related to data preprocessing, support for the conclusions remains incomplete. I also believe that a more careful interpretation of the "energy" derived from the maximum entropy model would greatly clarify what the analysis actually revealed.
(1) Major Comment 1:
I think the method used for binarization of BOLD activity is problematic in multiple ways.
a) Although the authors appear to avoid using global signal regression (page 4, lines 114-118), the proposed method effectively removes the global signal. According to the description on page 4, lines 117-122, the authors binarized network-wise ROI signals by comparing them with the cross-network BOLD signal (i.e., the global signal): at each time point, network-wise ROI signals above the cross-network signal were set to 1, and the rest were set to −1. If I understand the binarization procedure correctly, this approach forces the cross-network signal to be zero (up to some noise introduced by the binarization of network-wise signals), which is essentially equivalent to removing the global signal. Please clarify what the authors meant by stating that "this approach maintained a diverse range of binarized cortical states in data where the global signal was preserved" (page 4, lines 121-122).
b) The authors might argue that they maintained a diverse range of cortical states by performing the binarization at each time point (rather than within each network). However, I believe this introduces another problem, because binarizing network-wise signals at each time point distorts the distribution of cortical states. For example, because the cross-network signal is effectively set to zero, the network cannot take certain states, such as all +1 or all −1. Similarly, this binarization biases the system toward states with similar numbers of +1s and −1s, rather than toward unbalanced states such as (+1, −1, −1, −1, −1, −1). These constraints and biases are not biological in origin but are simply artifacts of the binarization procedure. Importantly, the energy landscape and its derivatives (e.g., hard/easy transitions) are likely to be affected by these artifacts. I suggest that the authors try a more conventional binarization procedure (i.e., binarization within each network), which is more robust to such artifacts.
Related to this point, I have a question regarding Figure S1, in which the authors plotted predicted versus empirical state probabilities. As argued above, some empirical state probabilities should be zero because of the binarization procedure. However, in Figure S1, I do not see data points corresponding to these states (i.e., there should be points on the y-axis). Did the authors plot only a subset of states in Figure S1? I believe that all states should be included. The correlation coefficient between empirical and predicted probabilities (and the accuracy) should also be calculated using all states.
c) The current binarization procedure likely inflates non-neuronal noise and obscures the relationship between the true BOLD signal and its binarized representation. For example, consider two ROIs (A and B): both (+2%, +1%) and (+0.01%, −0.01%) in BOLD signal changes would be mapped to (+1, −1) after binarization. This suggests that qualitatively different signal magnitudes are treated identically. I believe that this issue could be alleviated if the authors were to binarize the signal within each network, rather than at each time point.
(2) Major Comment 2:
As the authors state (page 5, lines 145-148), the "energy" described in the energy landscape is not biological energy but rather a statistical transformation of probability distributions derived from the Boltzmann distribution. If this is the case, I believe that Figure 2A is potentially misleading and should be removed. This type of schematic may give the false impression that cortical state dynamics are governed by the energy landscape derived from the maximum entropy model (which is not validated).
-
Reviewer #1 (Public review):
The authors analysed large-scale brain-state dynamics while humans watched a short video. They sought to identify the role of thalamocortical interactions.
Major concerns
(1) Rationale for using the naturalistic stimulus
In terms of brain state dynamics, previous studies have already reported large-scale neural dynamics by applying some data-driven analyses, like energy landscape analysis and Hidden Markov Model, to human fMRI/EEG data recorded during resting/task states. Considering such prior work, it'd be critical to provide sufficient biological rationales to perform a conceptually similar study in a naturalistic condition, i.e., not just "because no previous work has been done". The authors would have to clarify what type of neural mechanisms could be missed in conventional resting-state studies using, say, energy landscape analysis, but could be revealed in the naturalistic condition.
(2) Effects of the uniqueness of the visual stimulus and reproducibility
One of the main drawbacks of the naturalistic condition is the unexpected effects of the stimuli. That is, this study looked into the data recorded from participants who were watching Sherlock, but what would happen to the results if we analyzed the brain activity data obtained from individuals who were watching different movies? To ensure the generalizability of the current findings, it would be necessary to demonstrate qualitative reproducibility of the current observations by analysing different datasets that employed different movie stimuli. In fact, it'd be possible to find such open datasets, like www.nature.com/articles/s41597-023-02458-8.
(3) Spatial accuracy of the "Thalamic circuit" definition
One of the main claims of this study heavily relies on the accuracy of the localization of two different thalamic architectures: matrix and core. Given the conventional or relatively low spatial resolution of the fMRI data acquisition (3x3x3 mm^3), it appears to be critically essential to demonstrate that the current analysis accurately distinguished fMRI signals between the matrix and core parts of the thalamus for each individual.
(4) More detailed analysis of the thalamic circuits
In addition, if such thalamic localisation is accurate enough, it would be greatly appreciated if the authors perform similar comparisons not only between the matrix and core architectures but also between different nuclei. For example, anterior, medial, and lateral groups (e.g., pulvinar group). Such an investigation would meet the expectations of readers who presume some microscopic circuit-level findings.
(5) Rationale for different time window lengths
The authors adopted two different time window lengths to examine the neural dynamics. First, they used a 21-TR window for signal normalisation. Then, they narrowed down the window length to 13-TR periods for the following statistical evaluation. Such a seemingly arbitrary choice of the shorter time window might be misunderstood as a measure to relax the threshold for the correction of multiple comparisons. Therefore, it'd be appreciated if the authors stuck to the original 21-TR time window and performed statistical evaluations based on the setting.
(6) Temporal resolution
After identifying brain states with energy landscape analysis, this study investigated the brain state transitions by directly looking into the fMRI signal changes. This manner seems to implicitly assume that no significant state changes happen in one TR (=1.5sec), which needs sufficient validation. Otherwise, like previous studies, it'd be highly recommended to conduct different analyses (e.g., random-walk simulation) to address and circumvent this problem.
-
eLife Assessment
This study investigated the dynamics of human cortical network activity with functional magnetic resonance imaging during movie watching and studied the modulation of these dynamics by subcortical areas using an energy landscape mapping method. The authors identified a set of brain states defined at the level of canonical functional networks, quantified how the brain transitions between these states, and related transition probabilities to inter-subject correlations in evoked brain activity. A major emphasis of the work concerns the role of the thalamus, which shows transition-linked activity changes and dynamic connectivity patterns, including differential involvement of parvalbumin- and calbindin-associated thalamic subdivisions. The analytical strategy developed in this study is applicable to other task- and resting-state fMRI data and would be useful for many researchers in the field; however, the evidence supporting the overall conclusions remains incomplete due to limitations associated with fMRI data preprocessing, analysis, and cross-validation.
-
-
copenhagenizeindex.eu copenhagenizeindex.eu
-
Ranking of cities by how well cycling is organised / accomodated. In the European ranking (which is the same top 5 as the global one), Utrecht and Amsterdam, plus obv CPH itself, Gent and now Paris.
-
-
social-media-ethics-automation.github.io social-media-ethics-automation.github.io
-
nonymity can encourage inauthentic behavior because, with no way of tracing anything back to you1, you can get away with pretending you are someone you are not, or behaving in ways that would get your true self in trouble.
People only act like themselves when they are the ones to face the repercussions of their actions. Anonymity gives people the liberty from facing consequences therefore they tend to act more irrationally. Existentialism says that people are defined by their actions, but if no one ever knew who did them, then actions don't help define anyone.
-
-
momentummag.com momentummag.com
-
In 5 yrs Paris has doubled cycling's modal share, and become 5th ranking city in the Copenhagenize urban cycling index. Last summer ([[Paris Versailles 2025]]) we noticed the difference (compared to [[Paris 2021]] but also thought a lot still looked improvised not embedded yet. So probably some way until it's truly ingrained
-
-
md.giplt.nl md.giplt.nl
-
[[Diana Wildschut p]] guide to add a Heltec t114 to a solar powered garden light, so you can use it as a repeater outside.
-
-
www.biorxiv.org www.biorxiv.org
-
eLife Assessment
This study investigates whether heavy metal stress can induce maize-like phenotypic and molecular responses in teosinte and whether these responses overlap with genomic regions implicated in domestication. By combining copper and cadmium treatments with quantitative phenotyping, gene-expression analyses, and expanded assessments of nucleotide diversity across a key chromosome 5 interval, the authors provide an integrated view of how abiotic stress responses intersect with domestication-related traits. The significance of the findings is valuable, as the work offers meaningful insights for the subfield of maize evolution and stress biology by extending heavy-metal response analyses to teosinte and linking them to domestication-associated loci, although the evolutionary implications remain indirect. The strength of evidence is solid, with appropriately designed and quantitatively supported experiments that broadly support the claims, but do not yet establish a causal or historical role for heavy metal stress in domestication.
-
Reviewer #1 (Public review):
In this study, Acosta-Bayona et al. investigate whether heavy metal (HM) stress can induce phenotypic and molecular responses in teosinte parviglumis that resemble traits associated with domestication, and whether genes within a domestication-linked region show patterns consistent with reduced genetic diversity and signatures of selection. The authors exposed both maize and teosinte parviglumis to a fixed dose of copper and cadmium, representing an essential and a non-essential element, respectively. They assessed shoot and root phenotypic traits at a defined developmental stage in plants exposed to HM stress versus control. They then integrated these phenotypic results with expanded analyses of genetic diversity across a broader chromosome 5 interval, which was previously associated with domestication-related traits. Overall, the revisions improve the clarity and the robustness of the analyses, as well as make the conclusions better aligned with the evidence.
The revised manuscript is strengthened by several additions.
(1) The authors broaden the genetic analysis beyond a small set of loci and evaluate nucleotide variability across several genes within the linked chromosome 5 interval, which improves the interpretation of diversity patterns and reduces concerns about a too narrow locus selection or regional linkage effects driving the conclusions.
(2) The expression analyses are now presented with clearer methodological separation and stronger quantitative support. Now, tissue/developmental RT-PCR profiles are distinguished from real-time qPCR assays used to test HM-induced expression changes, with appropriate replication and statistical reporting.
(3) The authors include a transcriptome-scale element by analyzing multiple published and publicly available HM-stress transcriptome datasets and reporting shared differentially expressed genes across studies, which supports the interpretation that the observed expression changes align with broader HM-responsive transcriptional programs.
However, it remains challenging to distinguish which aspects of the HM responses observed here represent novel insight versus patterns already reported in maize HM-stress studies. In addition, the link between HM exposure and domestication history remains indirect: reduced diversity patterns and stress-responsive expression do not, on their own, demonstrate human-driven selection or a specific paleoenvironmental scenario, and alternative explanations related to general stress responses or regional evolutionary processes cannot be fully excluded.
-
Reviewer #2 (Public review):
Summary:
This work explores the phenotypic developmental traits associated with Cu and Cd responses in teosinte parviglumis, a species evolutionary related to extant maize crops. Cu and Cd could serve as a proxy for heavy metals present in the soils. The manuscript explores potential genetic loci associated with heavy metal responses and domestication. This includes heavy metal transporters which are unregulated during stress. To study that, authors compare the plant architecture of maize defective in ZmHMA1 and speculate on the association of heavy metals with domestication.
Strengths:
Very few studies covered the responses of teosintes to heavy metal stress. The physiological function of ZmHMA1 in maize is also valuable. The idea and speculation section is interesting and well-implemented.
Weaknesses:
Some conclusions are still speculative and future experiment could provide more clues about potential molecular mechanisms for the ideas proposed here.
-
Author response:
The following is the authors’ response to the original reviews
Public Reviews:
Reviewer #1(Public review):
In this study, Acosta-Bayona et al. aim to better understand how environmental conditions could have influenced specific gene functions that may have been selected for during the domestication of teosinte parviglumis into domesticated maize. The authors are particularly interested in identifying the initial phenotypic changes that led to the original divergence of these two subspecies. They selected heavy metal (HM) stress as the condition to investigate. While the justification for this choice remains speculative, paleoenvironmental data would add value; the authors hypothesize that volcanic activity near the region of origin could have played a role.
The justification of choice to investigate the effects of heavy metal stress is not speculative. As mentioned now in the Abstract, the elucidation of the genome from the Palomero toluqueño maize landrace revealed heavy metal effects during domestication (Vielle-Calzada et al., Science 2009). Our aim was to test the hypothesis that heavy metal (HM) stress influenced the evolutionary transition of teosinte parviglumis to maize.
(1) Although the paper presents some interesting findings, it is difficult to distinguish which observations are novel versus already known in the literature regarding maize HM stress responses. The rationale behind focusing on specific loci is often lacking. For example, a statistically significant region identified via LOD score on chromosome 5 contains over 50 genes, yet the authors focus on three known HM-related genes without discussing others in the region. It is unclear why ZmHMA1 was selected for mutagenesis over ZmHMA7 or ZmSKUs5.
We appreciated the depth and value of this comment.
Maize phenotypic responses to sublethal concentrations to heavy metals – copper (Cu) and cadmium (Cd) in particular - are well characterized and published, and in agreement with our results. In the first section of the Results (pgs 7 and 8), we added pertinent references to clearly show which observations are already known. By contrast, teosinte parviglumis responses are in all cases novel. To our knowledge this is the first study that analyzed in detail the phenotypic response of teosinte to sublethal concentrations of heavy metals, specifically Cu and Cd. We have now emphasized the novelty of these observations (pg 8).
To address the fact that we only focused on three known HM-related genes without discussing others in the statistically significant region identified via LOD score on chr.5, we have added a full section that reads as follows (pgs. 11 to 13 of the new version):
“Large-scale genomic and transcriptomic comparisons indicate that many HM response genes were positively selected across the maize genome.
To expand the results well beyond the analysis of the three genes previously described, we performed a detailed analysis of genetic diversity across the 11.47 Mb genomic region comprised between Z_mSKUs5_ and ZmHMA1. This additional analysis reveals general tendencies in the quantity and nature of loci that were affected by positive selection during the teosinte parviglumis to maize transition in a region identified via LOD score on chr.5. We compared nucleotide variability by using 100 bp bins covering loci composed of two 30 Kb segments up and downstream of coding sequences, respectively, and the coding sequence itself, for 173 genes present within the genomic region comprised between ZmSKUs5 and ZmHMA (Figure S1 and Supplementary File 6). Two types of statistical tests (ANOVA and Wilcoxon) were applied to nucleotide variability comparisons using the entirety of each locus. The Benjamini-Hochber procedure allowed an estimation of the false discovery rate (FDR<0.05) to avoid type I errors (false positives). Although some individual loci appear as differently classified depending on the statistical test applied (22 out of 173 loci), the general differences in nucleotide variability are consistently maintained within the subregions described below. We found that 166 out of 173 loci show signatures of positive selection and are roughly organized in five independent subregions of variable length. The first six loci are consecutively ordered in a 402 Kb subregion that includes ZmSKUs5. A second group of 13 consecutive loci expands over a 1.44 Mb subregion that contains NRAMP ALUMINUM TRANSPORTER1, also involved in HM response through uptake of divalent ions. A third group of 17 consecutive loci expands over 1.28 Mb; eleven contain genes encoding for uncharacterized proteins. The fourth group is composed of 57 consecutive loci expanding over 3.22 Mb and contains genes encoding for DEFECTIVE KERNEL55, AUXIN RESPONSE FACTOR16, and peroxydases involved in responses to oxydative stress. The fifth group contains 12 consecutive loci expanding over 713 Kb and contains ZmHMA1. An additional segment of approximately 1.17 Mb and containing 25 consecutive loci that were positively selected expands away from the ZmSKUs5-ZmHMA1 segment; it also contains several genes encoding for peroxydases. Although multiple loci include genes that could be involved in abiotic stress and oxidative responses, these results suggest that multiple factors other than HM stress could have played a role in the evolutionary mechanisms that affected the genetic diversity of chr.5 during the teosinte parviglumis to maize transition.
To further analyze the possibility that HM response could have played a role in maize emergence and subsequent domestication, we analyzed large scale transcriptomic data corresponding to independent experiments aiming at understanding the response of maize roots to HM stress. Six available transcriptomes were selected for in-depth analysis because they presented a fold change strictly higher than 1, and their results were supported by false discovery rates (FDR<0.05). These six transcriptomes (Table S5) included HM response datasets corresponding to growth conditions that not only incorporated Cu, but also lead (Pb) and chromium (Cr) that were not included in the substrate of our experiments. Transcriptional profiles were obtained from roots of plants at different stages: maize seedlings (Shen et al., 2012; Gao et al., 2015; Zhang et al., 2024a), three week old plantlets (Yang et al., 2023), and plants at V2 stage (Zhang et al., 2024b; Fengxia et al., 2025). A total of 120 genes shared by all six transcriptomes were found to be differentially expressed under HM stress conditions (66 upegulated and 54 downregulated; Figure S3), including ZmSKUs5, ZmHMA1 and ZmHMA7; 52 of them (43.3%) are located in maize loci showing less than 70% of the nucleotide variability found in teosinte parviglumis, suggesting that they were affected by positive selection (Yamasaki et al., 2005; Supplementary File 7). Of 18 mapping in chr.5, twelve are within the 82 cM that fractionates into multiple QTLs under selection during the parviglumis to maize transition. Interestingly, five additional loci containing HM response genes completely lack SNPs within their total length in both parviglumis and maize, and 19 additional loci lack SNPs in at least one 30 Kb segment or their coding region (Supplementary File 7), suggesting the frequent presence of ultraconserved genomic regions in many loci containing HM response genes. When this same analysis was conducted in a set of loci comprising 63 genes previously identified as differentially expressed in response to abiotic stress not directly related to HM responses (hypoxia; nutritional deficiency; soil alkalinity; drought; soil salinity), 18 loci (28.6%) showed less than 70% of the nucleotide variability found in teosinte parviglumis. Only one of them maps in chr.5 and none contained segments or coding regions lacking SNPs in parviglumis or maize. These results suggest that in contrast to other types of abiotic stress response genes, loci comprising a large set of genes that unambiguously respond to HM stress caused by chemical elements of diverse nature were affected by positive selection during the parviglumis to maize transition, irrespectively of their position in the genome.”
The detailed analysis of genetic diversity across 11.47 Mb of chr.5 in the genomic region comprised between ZmSKUs5 and ZmHMA1 in presented as Supplementary File 6.
The analysis of genetic diversity in loci encompassing heavy metal response genes shared by six transcriptomes and abiotic stress controls are described in Supplementary File 7.
In the Discussion (pgs. 21 and 22), we added a paragraph section that reads as follows:
“Although loss of genetic diversity is usually the result of human selection during domestication, it can also represent a consequence of natural selective pressures favoring fitness of specific teosinte parviglumis allelic variants better adapted to environmental changes and subsequently affected by human selection during the domestication process. This possibility is reflected by widely spread selective sweeps affecting a large portion of chr.5 that contains hundreds of genes showing signatures of positive selection. The analysis of 11.47 Mb covering the ZmHMA1ZmSKUs5 segment confirms the presence of large but discrete genomic subregions that were positively selected during the teosinte parviglumis to maize transition. Although several contain genes involved in HM response and oxidative stress, the diversity of gene functions does not necessarily favor abiotic stress over other factors that could be at the origin of selective forces affecting these regions. By contrast, a large scale transcriptomic survey indicates that genes consistently responding to HMs (Cu, Cd, Pb and Cr ) show signatures of positive selection at unusual high frequencies (43.3%) as compared to loci containing genes responding to other types of abiotic stress (28.6%). Our identification of HM response genes affected by positive selection is far from being exhaustive. Nevertheless, it agrees with the expected effects of a widespread selective sweep caused by environmental changes that influenced the parviglumis to maize transition at the genetic level. Of intriguing interest are 24 loci that partially or completely lack SNPs in both teosinte parviglumis and maize, suggesting possible genetic bottlenecks occurred before the teosinte to maize transition. Examples of other edaphological factors driving genetic divergence either in the teosintes or maize include local adaptation to phosphorus concentration in mexicana and parviglumis (Aguirre-Liguori et al. 2019), and fast maize adaptation to changing iron availability through the action of genes involved in its mobilization, uptake, and transport (Benke and Stich 2011). Our results reveal a teosinte parviglumis environmental plasticity that could be related to the function of HM response genes positively selected during the teosinte parviglumis to maize transition. Previous studies have demonstrated that transposable elements (TEs) contribute to activation of maize genes in response to abiotic stress, affecting up to 20% of the genes upregulated in response to abiotic stress, and as many as 33% of genes that are only expressed in response to stress (Makarevitch et al., 2015). It is therefore possible that the HM response of some specific genes that influenced maize emergence or domestication could be mediated by TEs influencing or driving their transcriptional regulation.”
The mutagenic analysis of ZmHMA7 and ZmSKUs5 will be included in a different publication.
(2) The idea that HM stress impacted gene function and influenced human selection during domestication is of interest. However, the data presented do not convincingly link environmental factors with human-driven selection or the paleoenvironmental context of the transition. While lower nucleotide diversity values in maize could suggest selective pressure, it is not sufficient to infer human selection and could be due to other evolutionary processes. It is also unclear whether the statistical analysis was robust enough to rule out bias from a narrow locus selection. Furthermore, the addition of paleoclimate records (Paleoenvironmental Data Sources as a starting point) or conducting ecological niche modeling or crop growth models incorporating climate and soil scenarios would strengthen the arguments.
We think that the detailed analysis of genetic diversity across 11.46 Mb covering the ZmSKUs5 to ZmHMA1 genomic segment – and its statistical validation - provides a precise understanding of the selective sweep dimensions in chr.5.
We do agree that lower nucleotide diversity values in maize are not sufficient to infer human selection. Because many HM response loci show unusually low nucleotide variability in teosinte parviglumis (see the results of the transcriptomic analysis presented above), we cannot discard the possibility that natural selection forces related to environmental changes could have affected native populations of teosinte parviglumis.
To further explore the link between environmental factors, natural or human-driven selection, and the paleoenvironmental context of the parviglumis to maize transition, we revised paleoenvironmental and geological records and added results in two sections that read as follows (pgs. 17 to 20):
“Paleoenvironmental studies reveal periods of climatic instability in the presumed region of maize emergence during the early Holocene.
It is well accepted that temperature fluctuations, volcanism and anthropogenic impact shaped the distribution and abundance of plant species in the Transmexican Volcanic Belt (TMVB) during the last 14,000 years (Torrescano-Valle et al. 2019). The TMVB has produced close to 8000 volcanic structures (Ferrari et al., 2011), transforming the relief multiple times, and causing hydrographic and soil changes that actively modified the distribution and composition of plant communities in Central Mexico. Detailed paleoenvironmental data for the Pleistocene and Holocene is available for several lacustrine zones located within the 50 to 100 km range of the region currently considered the cradle of maize domestication (Matzuoka et al. 2002; Figure 5a). In Lake Zirahuén (102°44′ W; 19°26′ N and approximately 2075 meters above sea level; index [i] in Figure 5a), pollen, microcharcoal and magnetic susceptibility analyses of two sedimentary sequences reveals three periods of major ecological change during the early and middle Holocene.
Between 9500 and 9000 calibrated years before present (cal yr BP), pine forests seem to have been associated with summer insolation increases. A second peak of forest change occurred at around 8200 cal yr BP, coinciding with cold oscillations documented in the North Atlantic. Finally, events occurred between 7500 and 7100 cal yr BP shows an abrupt change in the plant community related to humid Holocene climates and a presumed volcanic event (Lozano-García et al., 2013). The environmental history of the central Balsas watershed has also been documented by pollen, charcoal, and sedimentary analysis conducted in three lakes and a swamp of the Iguala valley (Piperno et al. 2007). Paleoecological records of lake Ixtacyola (8°20N, 99°35W and approximately 720 meters above sea level; index [ii] in Figure 5a) and lake Ixtapa (8°21N, 99°26W) indicate that an important increase in temperature and precipitation occurred between 13000 and 10000 cal yr BP. The pollen record of Ixtacyola showed that members of the genus Zea were already part of the vegetation coverage by 12900 to 13000 cal yr BP, suggesting that some teosintes – likely including parviglumis - were commonly found at elevation areas where they do not presently occur. Lake Almoloya (also named Chignahuapan; 19°05N, 99°20E and approximately 2575 meters above sea level; index [iii] in Figure 5a) in the upper Lerma basin is only 20 Km from the crater of the Nevado de Toluca that is responsible for creating the late Pleistocene Upper Toluca Pumice layer over which the Lerma basin is deposited. Pollen records indicate the presence of Zea species by 11080 to 10780 cal yr BP. As for other locations, an important period of climatic instability prevailed between 11500 and 8500 cal yr BP (Ludlow-Wiechers et al., 2005). Humidity fluctuations occurred until 8000 cal yr BP, with a stable temperate climate between 8500 and 5000 cal yr BP. Although pollen and diatom studies are often difficult to interpret at a regional scale, the overall results presented above suggest consistent periods of Zea plants present in periods of environmental and climatic instability that correlate with the history of volcanic activity during the early Holocene, as described in the next section.
Temporal and geographical convergence between volcanic eruptions and maize emergence during the Holocene.
Current evidence indicates that the emergence and domestication of maize initiated in Mesoamerica some time around 9,000 yr BP (Matsuoka et al. 2002). The current location of teosinte parviglumis populations that are phylogenetically most closely allied with maize are currently distributed in a region located between the Michoacan-Guanajuato Volcanic Field (MGVF) at their northwest, and the Nevado de Toluca and Popocatéptl volcanoes at their east and northeast (Figure 5a; Matsuoka et al. 2002). Precise records of field data indicate that ten accessions were collected in the Balsas river drainage near Teloloapan and Sierra de Huautla (Guerrero), at approximately 100 km south of the Nevado de Toluca crater. Three other accessions were collected near Tejupilco de Hidalgo and Zacazonapan (Estado de México), at approximately 50 to 60 km from the Nevado de Toluca crater (8762, JSG y LOS-161, and JSG-391). And four other accessions were located in Michoacan, at a location within the MGVF (accession 8763), or at mid-distance between the MGVF and the Nevado de Toluca crater (accessions JSG y LOS-130, 8761, and 8766).
The most important source of HMs in ancient soils of Mesoamerica is TMBV-dependent volcanic activity through short- and long-term effects related to lava deposits, ores, hydrothermal flow, and ash (Torrescano-Valle et al. 2019). The Nevado de Toluca volcano produced one of the most powerful eruptions from central Mesoamerica in the Holocene, giving rise to the Upper Toluca Pumice deposit at 12621 to 12025 cal yr BP (Arce et al., 2003; Figure 5b). The pumice fallout blanketed the Lerma and Mexico basins with 40 cm of coarse ash (Bloomfield and Valastro 1977; Arce et al. 2003). A second eruption dated by 36Cl exposure occurred at 9700 cal yr BP (Arce et al. 2003; Figure 5b), and the most recent eruption occurred at 3580 to 3831 cal yr BP (Macías et al. 1997). During the early and middle Holocene, the Popocatéptl volcano produced at least four eruptions dated 13037-12060, 10775–9564, 8328-7591, and 6262-5318 cal yr BP (Siebe et al. 1997); three other important eruptions occurred during the late Holocene, between 2713 and 733 cal yr BP (Siebe and Macías, 2006). In addition, the MGFV is a monogenetic volcanic field for which 23 independent eruptions have been documented during the Holocene, 21 of them located towards the southern part of the field, in close proximity to the region harboring some of the teosinte parviglumis populations most closely related to maize. Three of these eruptions occurred in the early Holocene (El Huanillo 1130 to 9688 cal yr BP; La Taza 10649 to 10300 cal yr BP; Cerro Grande 10173 to 9502 cal yr BP; Figure 5b), and three others during the initial period of the middle Holocene, between 8400 and 7696 cal yr BP (La Mina, Los Caballos, and Cerro Amarillo; Figure 5b). On average, a new volcano forms every ~435 years in the MGFV (Macías and Arce, 2019). No less than 16 other eruptions occurred between 7159 cal yr BP and the present time (Figure 5b). Soils of volcanic origin (andosols) are currently distributed in regions north-west from the Nevado de Toluca and Popocatéptl craters, in close proximity with teosinte parviglumis populations most closely related to maize (Figure S5). Although modern distribution of teosinte populations may differ from their distribution around 9000 yr BP, and unknown populations more closely related to maize may yet to be discovered, this data indicates that the date and region where maize emerged is convergent with the dates and locations of several volcanic eruptions occurred during the Holocene in that same region.”
(3) Despite the interest in examining HM stress in maize and the presence of a pleiotropic phenotype, the assessment of the impact of gene expression is limited. The authors rely on qPCR for two ZmHMA genes and the locus tb1, known to be associated with maize architecture. A transcriptomic analysis would be necessary to 1- strengthen the proposed connection and 2- identify other genes with linked QTLs, such as those in the short arm of chromosome 5.
Real-time qPCR is an accurate and reliable approach to assess the expression of specific genes such as ZMHMA1 and Tb1, but we agree that our results do not allow to establish a direct regulatory link between the function of Tb1, the pleiotropic parviglumis phenotype under HM stress, and the function of ZmHMA1. We also concede that the large transcriptional analysis of HM response in maize (presented above) does not allow to elucidate a possible connection between these two genes. We have substantially downplayed our conclusion in this section by modifying the end of the section in pg. 17, that now reads:
“These results do not allow to directly link the regulation of ZmHMA1 expression to the function of Tb1; however, they open an opportunity to further investigate the possibility that under HM stress, the formation of secondary ramifications in teosinte parviglumis could be repressed by transcription factors of the TCP family, including Tb1.”
This is also emphasized in the Discussion (pg 21) as follows:
“Under HM stress, we also show that Tb1 is overexpressed in the apical meristem of teosinte parviglumis, suggesting that formation of secondary ramifications is repressed by Tb1 function under HM stress, as in extant maize. At this stage we cannot discard the possibility that Tb1 upregulation in parviglumis reflects a more generalized response to abiotic stress; however, the expression ZmHMA1 is downregulated in W22 wild-type maize meristems in the presence of HMs but upregulated in teosinte parviglumis meristems, suggesting that a specific regulatory shift relating HM responses and ZmHMA1 function occurred during the teosinte parviglumis to maize transition.”
On the other hand, the transcriptional analysis the identification of 52 additional HM response genes showing signatures of positive selection occurred during the parviglumis to maize transition; 12 of them map to chr.5 within the region having linked QTLs within the short arm of chr.5. So far, genes involved in HM response and oxidative stress represent the most prevalent class of genes identified within the genomic region showing pleiotropic effects on domestication and multiple linked QTLs in chr.5.
Reviewer #2 (Public review):
Summary:
This work explores the phenotypic developmental traits associated with Cu and Cd responses in teosinte parviglumis, a species evolutionary related to extant maize crops. Cu and Cd could serve as a proxy for heavy metals present in the soils. The manuscript explores potential genetic loci associated with heavy metal responses and domestication identified in previous studies. This includes heavy metal transporters, which are unregulated during stress. To study that, the authors compare the plant architecture of maize defective in ZmHMA1 and speculate on its association with domestication.
Strengths:
Very few studies covered the responses of teosintes to heavy metal stress. The physiological function of ZmHMA1 in maize also gives some novelty in this study. The idea and speculation section is interesting and well-implemented.
Weaknesses:
The authors explored Cu/Cd stress but not a more comprehensive panel of heavy metals, making the implications of this study quite narrow. Some techniques used, such as end-point RT-PCR and qPCR, are substandard for the field. The phenotypic changes explored are not clearly connected with the potential genetic mechanisms associated with them, with the exception of nodal roots. If teosintes in response to heavy metal have phenotypic similarity with modern landraces of maize, then heavy metal stress might have been a confounding factor in the selection of maize and not a potential driving factor. Similar to the positive selection of ZmHMA1 and its phenotypic traits. In that sense, there is no clear hypothesis of what the authors are looking for in this study, and it is hard to make conclusions based on the provided results to understand its importance. The authors do not provide any clear data on the potential influence of heavy metals in the field during the domestication of maize. The potential role of Tb-1 is not very clear either.
Thank you for these comments. We have now emphasized our hypothesis in the abstract and the last paragraph of the Introduction (pg. 6):
“To test the hypothesis that heavy metal (HM) stress influenced the evolutionary transition of teosinte to maize, we exposed both subspecies to sublethal concentrations of copper and cadmium etc…”
A comprehensive panel of heavy metals would not be more accurate in terms of simulating the composition of soils evolving across 9,000 years in the region where maize presumably emerged. Copper (Cu) and cadmium (Cu) correspond each to a different affinity group for proteins of the ZmHMA family. ZmHMA1 has preferential affinity for Cu and Ag (silver), whereas ZmHMA7 has preferential affinity to Cd, Zn (zinc), Co (cobalt), and Pb (lead). Since these P1b-ATPase transporters mediate the movement of divalent cations, their function remains consistent regardless of the specific metal tested, provided it belongs to the respective affinity group. By applying sublethal concentrations of Cd (16 mg/kg) and Cu (400 mg/kg), we caused a measurable physiological response while allowing plants to complete their life cycle, including the reproductive phase, facilitating a comprehensive analysis of metal stress adaptation. Whereas higher doses impair flowering or are lethal, lower Cu/Cd concentrations do not consistently show conventional phenotypic responses such as reduced plant growth (AbdElgawad et al. 2020; Atta et al., 2023)
Based on comments by both reviewers, we present now a large transcriptional analysis that incorporates HM responses to lead (Pb) and chromium (Cr), in addition to Cu. Results show that many genes responding to Pb and Cr were also positively selected across the maize genome, suggesting that HM stress led to a ubiquitous rather than a specific evolutionary response to heavy metals (please see our response to Reviewer#1 and sections in pgs. 11 to 13) .
Real-time qPCR is an accurate and reliable approach to assess the expression of specific genes such as ZMHMA1 and Tb1, but we agree that our results do not allow to establish a direct regulatory link between the function of Tb1, the pleiotropic parviglumis phenotype under HM stress, and the function of ZmHMA1. We also concede that the large transcriptional analysis of HM response in maize (presented above) does not allow to elucidate a possible connection between these two genes. Therefore, we have substantially downplayed our conclusion in this section by modifying the end of the section in pg. 17, that now reads:
“These results do not allow to directly link the regulation of ZmHMA1 expression to the function of Tb1; however, they open an opportunity to further investigate the possibility that under HM stress, the formation of secondary ramifications in teosinte parviglumis could be repressed by transcription factors of the TCP family, including Tb1.”
There are two phenotypic changes clearly connected with the genetic mechanisms involved in the parviglumis to maize transition: plant height and the number of seminal roots (not nodal roots). These changes have been now emphasized in the Abstract and the description of the results.
Regarding the possibility for HM stress to represent a confounding factor in the selection of maize and not a driving factor, we expanded the genomic analysis of genetic diversity well beyond the analysis of the three genes under initial study, to cover a segment of 11.47 Mb comprised between ZmSKUs5 and ZmHMA1. We compared nucleotide variability by using 100 bp bins covering loci composed of two 30 Kb segments up and downstream of coding sequences, respectively, and the coding sequence itself, for 173 genes present within the genomic region comprised between ZmSKUs5 and ZmHMA (Figure S1 and Supplementary File 6). The full analysis is presented in a new section pgs. 11 and 12. We found that 166 out of 173 loci show signatures of positive selection and are roughly organized in five independent subregions of variable length. Four out of five subregions contain more than one HM or oxidative stress response gene within loci showing signatures of positive selection. Although multiple factors other than HM stress could have played a role in the evolutionary mechanisms that affected the genetic diversity of chr.5, large scale transcriptomic data corresponding to independent experiments aiming at understanding the response of maize roots to HM stress allowed the identification of 49 additional HM response genes within loci showing positive selection across the genome, a proportion (43.3%) far greater than the proportion of loci containing response genes to other types of abiotic stress not related to HMs (28.6%). These results are described in detail in pgs. 12 and 13 (Figure S3 and Supplementary File 7). These results provide strong evidence in favor of HM stress and not another factor driving positive selection.
We now provide precise and pertinent paleoenvironmental data on the potential influence of heavy metals in the field. In sections pgs. 17 to 20 we review paleoenvironmental studies revealing periods of climatic instability in the presumed region of maize emergence during the early Holocene, and data indicating that the date and region where maize emerged is convergent with the dates and locations of several volcanic eruptions occurred during the early and middle Holocene in that same region. Please see responses to Reviewer#1 for details.
We agree that our results do not allow to establish a direct regulatory link between the function of Tb1, the pleiotropic parviglumis phenotype under HM stress, and the function of ZmHMA1. We also concede that the large transcriptional analysis of HM response in maize (presented above) does not allow to elucidate a possible connection between these two genes. Therefore, we have substantially downplayed our conclusion in this section by modifying the end of the section in pg. 17, that now reads:
“These results do not allow to directly link the regulation of ZmHMA1 expression to the function of Tb1; however, they open an opportunity to further investigate the possibility that under HM stress, the formation of secondary ramifications in teosinte parviglumis could be repressed by transcription factors of the TCP family, including Tb1.”
This is also emphasized in the Discussion (pg 21) as follows:
“Under HM stress, we also show that Tb1 is overexpressed in the apical meristem of teosinte parviglumis, suggesting that formation of secondary ramifications is repressed by Tb1 function under HM stress, as in extant maize. At this stage we cannot discard the possibility that Tb1 upregulation in parviglumis reflects a more generalized response to abiotic stress; however, the expression ZmHMA1 is downregulated in W22 wild-type maize meristems in the presence of HMs but upregulated in teosinte parviglumis meristems, suggesting that a specific regulatory shift relating HM responses and ZmHMA1 function occurred during the teosinte parviglumis to maize transition.”
Recommendations for the authors:
Reviewer #1 (Recommendations for the authors):
While the dataset generated provides an interesting foundation for hypothesis testing on HM stress and domestication, the current data do not sufficiently support the conclusions of the manuscript.
(1) The description of maize and teosinte architecture under HM stress is well presented.
However, traits like shoot height, leaf size reduction, and biomass loss also occur under other environmental stresses such as drought and salinity. Additional evidence beyond shoot and root architecture would help validate the link between tb1 expression and specific ZmHMA genes under HM stress, or whether it reflects a more generalized stress response.
We have already addressed in detail this point in the public response to Reviewer#1.
(2) The nucleotide variability analysis is interesting, but I would have liked to see additional information to clarify the choice of the data selection and the strength of the conclusions with human selection.
We have already addressed in detail this point in the public response to Reviewer#1.
a) The choice of Tripsacum dactyloides as the outgroup to determine nucleotide variability seems to be distant, and I wonder whether other combinations with a closer outgroup or multiple outgroups were tried to provide a more accurate context.
Nucleotide variability in Tripsacum dactyloides is used to graphically illustrate an external reference and not as an outgroup in the extended analysis of genetic diversity at the locus and genomic level. We did not used Tripsacum dactyloides as an outgroup in our statisticalm analysis. We could have indeed a closer teosinte subspecies as an outgroup, but at this stage no data warrants that environmentally-related selective pressures could have affected genetic diversite in other teosintes. This possibility in currently being investigated.
b) Evolutionary differences not related to human influence could affect the results. The phrase "order of magnitude difference in π values" needs statistical validation (e.g., confidence intervals, p-values).
We agree and have eliminated the sentence, as it is no longer relevant at the light of the detailed genomic analysis of genetic diversity prsented in Supplementary File 6.
c) The comparison with ZmGLB1, a neutral control locus, suggests that domestication-related changes in nucleotide variability are specific to the three candidate genes. However, the concept of neutrality is complex, and while ZmGLB1 may be considered neutral in this case, the argument does not address the possibility of other factors, such as linked selection, that could influence variability in these genes. Referencing Hufford et al. is insufficient and would require a deeper argument.
We also agree with this comment. We think that the influence and consequences of linked selection are now well documented for 11.46 Mb analyzed in chr.5 (pgs 11 and 12) in the main text and Supplementary File 6).
(3) The statement: "Our evidence indicates that HM stress revealed a teosinte parviglumis environmental plasticity that is directly related to the function of specific HM response genes that were affected by domestication through human selection" is not supported by the presented data. The rationale for the specific Cd/Cu dosage used is unclear. A dose-response gradient would better demonstrate the nature and strength of the plastic response.
Previous reports support the rationale for the specific HM dosage in this study; Cu/Cd dosage response gradients have been conducted in maize (AbdElgawad et al. 2020; Atta et al., 202), but since no studies have been conducted in teosinte, we reasoned that it was important to apply the same treatment to both subspecies. We have now emphasized this rationale by adding the following in pg XX: “Whereas higher doses impair flowering or are lethal, lower Cu/Cd concentrations do not consistently show conventional phenotypic responses such as reduced plant growth (AbdElgawad et al. 2020; Atta et al., 2023)”.
We agree that the statement raised by the reviewer needed revision at the light of our results. We did revise the statement to accurately reflect our current evidence as follows: “Our results reveal a teosinte parviglumis environmental plasticity that is likely related to the function of HM response genes positively selected during the teosinte parviglumis to maize transition.”
(4) In maize, TEs are known to influence gene expression under abiotic stress, including for tb1 (PMID: 25569788). Since the author appears to make a causative conclusion between ZmHMA1, TB1, and HM stress, I would have liked to see a whole-transcriptome analysis and not a curation of two genes to determine whether other factors, such as TEs, can have that would lead to similar outcomes.
We agree that is definetely a possibility that we have not investigated at this stage. However, we added a pargraph to reflect this pertinent suggestion:
“Previous studies have demonstrated that transposable elements (TEs) contribute to activation of maize genes in response to abiotic stress, affecting up to 20% of the genes upregulated in response to abiotic stress, and as many as 33% of genes that are only expressed in response to stress (Makarevitch et al., 2015). It is therefore possible that the HM response of some specific genes that influenced maize emergence or domestication could be mediated by TEs influencing or driving their transcriptional regulation.”
(5) I would suggest that the authors carefully review the tables, figures, and the corresponding legends. For example :
a) Table 2 is called before Table 1, I would therefore suggest changing the numbering to reflect the paragraph order.
Thank you for your help, we did change the order of the Tables in the new version.
b) In Table 2, it is not clear whether the P value applies to the mean difference between WT and the mutant zmhma1, either in the presence or the absence of heavy metals. In addition, the authors need to use the P-value to estimate the differences between WT in the absence vs presence of HM, and WT in the absence of HM versus the mutant in the absence of HM (idem for presence).
We did address this issue in detail and added P-values and specific pairwise comparisons to that Table (now Table 1). Data are presented as mean ± standard deviation and were tested by a paired Student’s T-Test. When the effects were significant according to T-Test, the treatments were compared with the Welch two sample T-Test at P < 0.05.
c) Table 1 and Table 2: Indicate what type of statistical test was used and the number of plants used for each experiment (n). Also, I recommend the use of scientific notation for the P-values.
The statistical tests have now been indicated, scientific notation has been added to the P-values; the number of plants and biological replicates are indicated in the Methods section.
d) Lines 202 and 204: I assume Table 1 should be called instead of Table 2.
This error has been corrected.
e) General: In the text, when significance is highlighted along with measurements, the p-value needs to be added.
We have added the P-value along the measurement for all significant differences.
f) In the text, it is also mentioned that "the expression of ZMHMA1 was significantly increased in the presence of HMs (Figure 3c)". We are looking here at an RT-PCR, which is qualitative and without a robust quantitative comparison and statistics, I cannot conclude this assessment based on the presented evidence. No statistical measure is indicated here.
Panel 3c is not RT-PCR but a real-time qPCR, showing relative fold-change, normalized to actin, with a 3-technical triplicate per 3 biological replicates). We have added error bars (SD) and P-values represented by asterisks (calculated with Student's t statistic) to support significant differences (P<0.05 and P<0.01). ZmHMA1 expression was significantly increased in the presence of HMs only in teosinte; there was no significant difference in maize.
g) Figure 3 should at least have the gene name in the figure to quickly understand the figure panel. The key conserved domains should also be identified.
We agree and apologize for the omission. The gene names have been added adjacent to the structures.
h) Sentence at lines 459-460 lacks words and punctuation.
This unfortunate rror has also been corrected.
i) Figure S1, the reference Lemmon and Doebley, 2024 should be Lemmon and Doebley, 2014 to harmonize with the text.
The correct year is 2014. We have corrected this error.
Reviewer #2 (Recommendations for the authors):
(1) The narrative should be clearer, starting with a clearer hypothesis that is later sustained or not in the results, and then discussed in the idea and speculation section.
Thank you for the comment. We have clarified the hypothesis, it is included in the abstract and the last paragraph of the Introduction. We hope it is now clear that the evidence presented supports our hypothesis
(2) Focus more on traits that are relevant, for example, nodal and seminal roots.
We modified the text to emphasize three relevant traits. In the case of teosinte under HM stress, absence of tillering and increase in the number of female inflorescences. In the case of the zmha1 mutant under HM stress, differences in the number of nodal roots, and differences in height.
(3) RNA-seq in Cu/Cd stress could make the work much more useful and complete.
As previously mentioned, we have incorporated a large scale transcriptional analysis on the basis of six transcriptomes statistically validated (Table S5). Please see sections pgs. 11 to 13 for details.
-
-
social-media-ethics-automation.github.io social-media-ethics-automation.github.io
-
And they also talked about the advertising motives behind supporting social causes (even if some employees do indeed support them), and the advertising motivation behind tweeting openly about how they are basing their decisions based on advertising.
I never see them doing this as an issue, as behind the screen of who is running the brand account is also a human, and that being able to break free from professionalism and connecting with people online, and express their opinions can be seen as a good thing, but also it can be a brilliant marketing strategy. With many brands being able to relate to and speak about the problems today help show that the corporation also cares about the people, which can help them gain more supporters and customers. But sometimes, if the topic is really controversial, or something that shouldn't be said online, some companies will still speak on it, which may hurt their companies image.
-
-
human.libretexts.org human.libretexts.org
-
in plays the audience often becomes part of the show
In a musical like the 2021 revival of Cabaret the plot of the show is set inside of a 1930's cabaret club, which the actual London theater is dressed up to look like, bringing the audience into the world of the show.
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
137805
DOI: 10.7554/eLife.105086
Resource: RRID:Addgene_137805
Curator: @olekpark
SciCrunch record: RRID:Addgene_137805
-
32445
DOI: 10.7554/eLife.105086
Resource: RRID:Addgene_32445
Curator: @olekpark
SciCrunch record: RRID:Addgene_32445
-
64853
DOI: 10.7554/eLife.105086
Resource: RRID:Addgene_64853
Curator: @olekpark
SciCrunch record: RRID:Addgene_64853
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
12251
DOI: 10.7554/eLife.104545
Resource: RRID:Addgene_12251
Curator: @olekpark
SciCrunch record: RRID:Addgene_12251
-
50661
DOI: 10.7554/eLife.104545
Resource: RRID:Addgene_50661
Curator: @olekpark
SciCrunch record: RRID:Addgene_50661
-
126679
DOI: 10.7554/eLife.104545
Resource: RRID:Addgene_126679
Curator: @olekpark
SciCrunch record: RRID:Addgene_126679
-
223959
DOI: 10.7554/eLife.104545
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_223959
-
223965
DOI: 10.7554/eLife.104545
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_223965
-
12253
DOI: 10.7554/eLife.104545
Resource: RRID:Addgene_12253
Curator: @olekpark
SciCrunch record: RRID:Addgene_12253
-
8454
DOI: 10.7554/eLife.104545
Resource: RRID:Addgene_8454
Curator: @olekpark
SciCrunch record: RRID:Addgene_8454
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
pMD2G
DOI: 10.7150/thno.120935
Resource: RRID:Addgene_12259
Curator: @olekpark
SciCrunch record: RRID:Addgene_12259
-
psPAX2
DOI: 10.7150/thno.120935
Resource: RRID:Addgene_12260
Curator: @olekpark
SciCrunch record: RRID:Addgene_12260
-
NLS-mCherry-NES reporter (pDN160)
DOI: 10.7150/thno.120935
Resource: RRID:Addgene_72660
Curator: @olekpark
SciCrunch record: RRID:Addgene_72660
-
pCMV-HA
DOI: 10.7150/thno.120935
Resource: Addgene (RRID:SCR_002037)
Curator: @olekpark
SciCrunch record: RRID:SCR_002037
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
175281
DOI: 10.64898/2026.01.08.698485
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_175281
-
210730
DOI: 10.64898/2026.01.08.698485
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_210730
-
175273
DOI: 10.64898/2026.01.08.698485
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_175273
-
175280
DOI: 10.64898/2026.01.08.698485
Resource: RRID:Addgene_175280
Curator: @olekpark
SciCrunch record: RRID:Addgene_175280
-
175274
DOI: 10.64898/2026.01.08.698485
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_175274
-
175277
DOI: 10.64898/2026.01.08.698485
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_175277
-
175278
DOI: 10.64898/2026.01.08.698485
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_175278
-
175279
DOI: 10.64898/2026.01.08.698485
Resource: RRID:Addgene_175279
Curator: @olekpark
SciCrunch record: RRID:Addgene_175279
-
175276
DOI: 10.64898/2026.01.08.698485
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_175276
-
179952
DOI: 10.64898/2026.01.08.698485
Resource: RRID:Addgene_179952
Curator: @olekpark
SciCrunch record: RRID:Addgene_179952
-
179953
DOI: 10.64898/2026.01.08.698485
Resource: RRID:Addgene_179953
Curator: @olekpark
SciCrunch record: RRID:Addgene_179953
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
72248
DOI: 10.64898/2025.12.20.695720
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_72248
-
117919
DOI: 10.64898/2025.12.20.695720
Resource: RRID:Addgene_117919
Curator: @olekpark
SciCrunch record: RRID:Addgene_117919
-
70708
DOI: 10.64898/2025.12.20.695720
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_70708
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
59358
DOI: 10.64898/2025.12.15.694023
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_59358
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
12253
DOI: 10.64898/2025.12.11.693673
Resource: RRID:Addgene_12253
Curator: @olekpark
SciCrunch record: RRID:Addgene_12253
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
241213
DOI: 10.64898/2025.12.10.693484
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_241213
-
200550
DOI: 10.64898/2025.12.10.693484
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_200550
-
82577
DOI: 10.64898/2025.12.10.693484
Resource: RRID:Addgene_82577
Curator: @olekpark
SciCrunch record: RRID:Addgene_82577
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
50474
DOI: 10.64898/2025.12.01.691673
Resource: RRID:Addgene_50474
Curator: @olekpark
SciCrunch record: RRID:Addgene_50474
-
50475
DOI: 10.64898/2025.12.01.691673
Resource: RRID:Addgene_50475
Curator: @olekpark
SciCrunch record: RRID:Addgene_50475
-
114472
DOI: 10.64898/2025.12.01.691673
Resource: RRID:Addgene_114472
Curator: @olekpark
SciCrunch record: RRID:Addgene_114472
-
AAV5-hsyn-DIO-hM3Dq
DOI: 10.64898/2025.12.01.691673
Resource: RRID:Addgene_44361
Curator: @olekpark
SciCrunch record: RRID:Addgene_44361
-
AAVrg-hSyn-Cre
DOI: 10.64898/2025.12.01.691673
Resource: RRID:Addgene_105553
Curator: @olekpark
SciCrunch record: RRID:Addgene_105553
-
50459
DOI: 10.64898/2025.12.01.691673
Resource: RRID:Addgene_50459
Curator: @olekpark
SciCrunch record: RRID:Addgene_50459
-
105540
DOI: 10.64898/2025.12.01.691673
Resource: RRID:Addgene_105540
Curator: @olekpark
SciCrunch record: RRID:Addgene_105540
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
45770
DOI: 10.4062/biomolther.2025.228
Resource: RRID:Addgene_45770
Curator: @olekpark
SciCrunch record: RRID:Addgene_45770
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
12259
DOI: 10.3892/ol.2025.15415
Resource: RRID:Addgene_12259
Curator: @olekpark
SciCrunch record: RRID:Addgene_12259
-
12260
DOI: 10.3892/ol.2025.15415
Resource: RRID:Addgene_12260
Curator: @olekpark
SciCrunch record: RRID:Addgene_12260
-
52961
DOI: 10.3892/ol.2025.15415
Resource: RRID:Addgene_52961
Curator: @olekpark
SciCrunch record: RRID:Addgene_52961
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
8941
DOI: 10.3390/cells14242016
Resource: RRID:Addgene_8941
Curator: @olekpark
SciCrunch record: RRID:Addgene_8941
-
115142
DOI: 10.3390/cells14242016
Resource: RRID:Addgene_115142
Curator: @olekpark
SciCrunch record: RRID:Addgene_115142
-
108294
DOI: 10.3390/cells14242016
Resource: RRID:Addgene_108294
Curator: @olekpark
SciCrunch record: RRID:Addgene_108294
-
32908
DOI: 10.3390/cells14242016
Resource: RRID:Addgene_32908
Curator: @olekpark
SciCrunch record: RRID:Addgene_32908
-
23252
DOI: 10.3390/cells14242016
Resource: RRID:Addgene_23252
Curator: @olekpark
SciCrunch record: RRID:Addgene_23252
-
86611
DOI: 10.3390/cells14242016
Resource: RRID:Addgene_86611
Curator: @olekpark
SciCrunch record: RRID:Addgene_86611
-
113096
DOI: 10.3390/cells14242016
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_113096
-
135276
DOI: 10.3390/cells14242016
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_135276
-
19772
DOI: 10.3390/cells14242016
Resource: RRID:Addgene_19772
Curator: @olekpark
SciCrunch record: RRID:Addgene_19772
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
242746
DOI: 10.17912/micropub.biology.001866
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_242746
-
244454
DOI: 10.17912/micropub.biology.001866
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_244454
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
216674/
DOI: 10.1371/journal.pbio.3003537
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_216674
-
216673/
DOI: 10.1371/journal.pbio.3003537
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_216673
-
216672/
DOI: 10.1371/journal.pbio.3003537
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_216672
-
216671/
DOI: 10.1371/journal.pbio.3003537
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_216671
-
216670/
DOI: 10.1371/journal.pbio.3003537
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_216670
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
12259
DOI: 10.1242/jcs.264444
Resource: RRID:Addgene_12259
Curator: @olekpark
SciCrunch record: RRID:Addgene_12259
-
12260
DOI: 10.1242/jcs.264444
Resource: RRID:Addgene_12260
Curator: @olekpark
SciCrunch record: RRID:Addgene_12260
-
247440
DOI: 10.1242/jcs.264444
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_247440
-
247439
DOI: 10.1242/jcs.264444
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_247439
-
247438
DOI: 10.1242/jcs.264444
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_247438
-
247437
DOI: 10.1242/jcs.264444
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_247437
-
41393
DOI: 10.1242/jcs.264444
Resource: RRID:Addgene_41393
Curator: @olekpark
SciCrunch record: RRID:Addgene_41393
-
247436
DOI: 10.1242/jcs.264444
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_247436
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
20972
DOI: 10.1242/jcs.264173
Resource: RRID:Addgene_20972
Curator: @olekpark
SciCrunch record: RRID:Addgene_20972
-
236912
DOI: 10.1242/jcs.264173
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_236912
-
12260
DOI: 10.1242/jcs.264173
Resource: RRID:Addgene_12260
Curator: @olekpark
SciCrunch record: RRID:Addgene_12260
-
52961
DOI: 10.1242/jcs.264173
Resource: RRID:Addgene_52961
Curator: @olekpark
SciCrunch record: RRID:Addgene_52961
-
31202
DOI: 10.1242/jcs.264173
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_31202
-
162823
DOI: 10.1242/jcs.264173
Resource: RRID:Addgene_162823
Curator: @olekpark
SciCrunch record: RRID:Addgene_162823
-
75161
DOI: 10.1242/jcs.264173
Resource: RRID:Addgene_75161
Curator: @olekpark
SciCrunch record: RRID:Addgene_75161
-
98291
DOI: 10.1242/jcs.264173
Resource: RRID:Addgene_98291
Curator: @olekpark
SciCrunch record: RRID:Addgene_98291
-
83480
DOI: 10.1242/jcs.264173
Resource: RRID:Addgene_83480
Curator: @olekpark
SciCrunch record: RRID:Addgene_83480
-
101278
DOI: 10.1242/jcs.264173
Resource: None
Curator: @olekpark
SciCrunch record: RRID:Addgene_101278
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
49386
DOI: 10.1242/jcs.264075
Resource: RRID:Addgene_49386
Curator: @olekpark
SciCrunch record: RRID:Addgene_49386
-
80975
DOI: 10.1242/jcs.264075
Resource: RRID:Addgene_80975
Curator: @olekpark
SciCrunch record: RRID:Addgene_80975
-
62987
DOI: 10.1242/jcs.264075
Resource: RRID:Addgene_62987
Curator: @olekpark
SciCrunch record: RRID:Addgene_62987
-
139054
DOI: 10.1242/jcs.264075
Resource: RRID:Addgene_139054
Curator: @olekpark
SciCrunch record: RRID:Addgene_139054
-
12260
DOI: 10.1242/jcs.264075
Resource: RRID:Addgene_12260
Curator: @olekpark
SciCrunch record: RRID:Addgene_12260
-
12259
DOI: 10.1242/jcs.264075
Resource: RRID:Addgene_12259
Curator: @olekpark
SciCrunch record: RRID:Addgene_12259
-
11795
DOI: 10.1242/jcs.264075
Resource: RRID:Addgene_11795
Curator: @olekpark
SciCrunch record: RRID:Addgene_11795
-
-
pmc.ncbi.nlm.nih.gov pmc.ncbi.nlm.nih.gov
-
11623
DOI: 10.1172/JCI194395
Resource: RRID:Addgene_11623
Curator: @olekpark
SciCrunch record: RRID:Addgene_11623
-
12260
DOI: 10.1172/JCI194395
Resource: RRID:Addgene_12260
Curator: @olekpark
SciCrunch record: RRID:Addgene_12260
-
12259
DOI: 10.1172/JCI194395
Resource: RRID:Addgene_12259
Curator: @olekpark
SciCrunch record: RRID:Addgene_12259
-
52961
DOI: 10.1172/JCI194395
Resource: RRID:Addgene_52961
Curator: @olekpark
SciCrunch record: RRID:Addgene_52961
-
99374
DOI: 10.1172/JCI194395
Resource: RRID:Addgene_99374
Curator: @olekpark
SciCrunch record: RRID:Addgene_99374
-