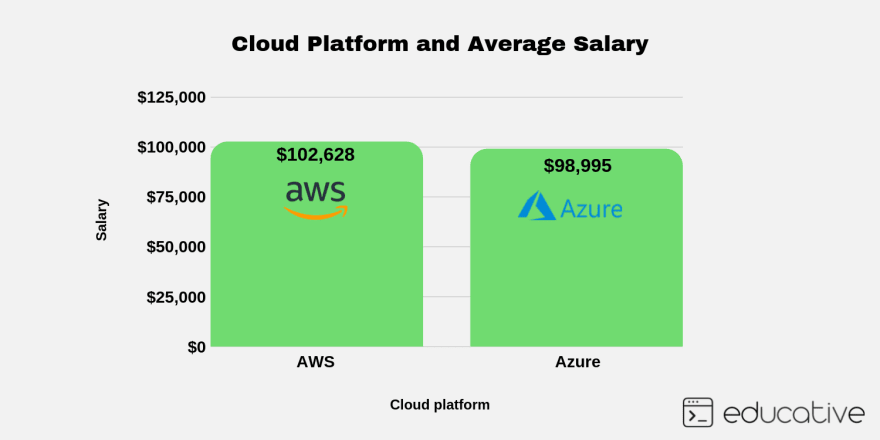
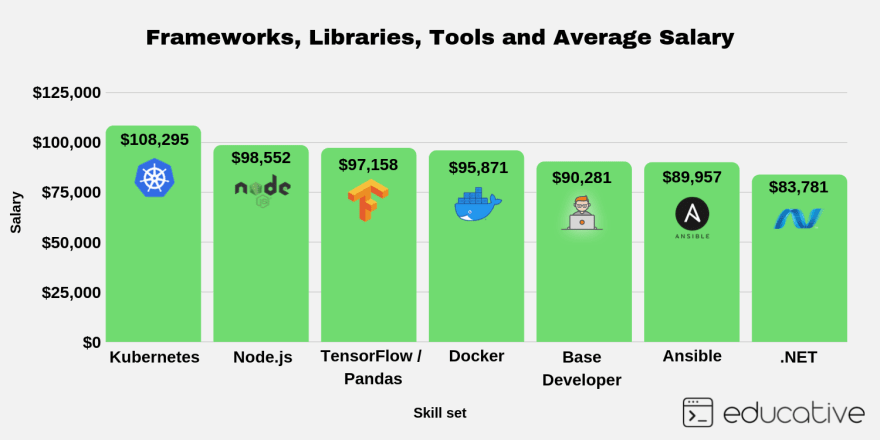
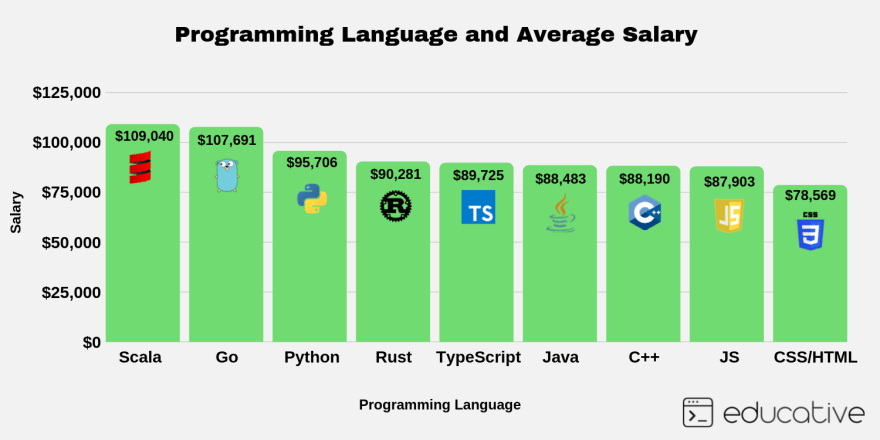
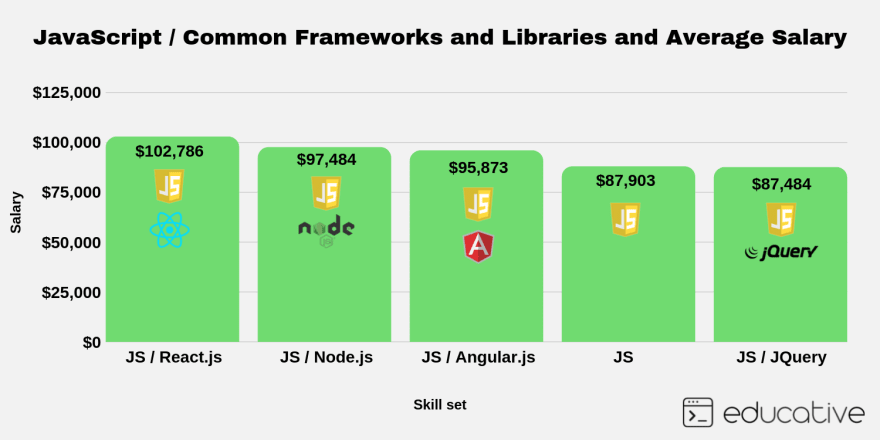
Simplified formula for the expected number of tosses (e) to get n consecutive heads (n≥1):
$$e_n=2(2^n-1)$$
For example, to get 5 consecutive heads, we've to toss the coin 62 times:
$$e_n=2(2^5-1)=62$$
We can also start with the longer analysis of the 5 scenarios:
- If we get a tail immediately (probability 1/2) then the expected number is e+1.
- If we get a head then a tail (probability 1/4), then the expected number is e+2.
- If we get two head then a tail (probability 1/8), then the expected number is e+2.
- If we get three head then a tail (probability 1/16), then the expected number is e+4.
- If we get four heads then a tail (probability 1/32), then the expected number is e+5.
- Finally, if our first 5 tosses are heads, then the expected number is 5.
Thus:
$$e=\frac{1}{2}(e+1)+\frac{1}{4}(e+2)+\frac{1}{8}(e+3)+\frac{1}{16}\\(e+4)+\frac{1}{32}(e+5)+\frac{1}{32}(5)=62$$
We can also generalise the formula to:
$$e_n=\frac{1}{2}(e_n+1)+\frac{1}{4}(e_n+2)+\frac{1}{8}(e_n+3)+\frac{1}{16}\\(e_n+4)+\cdots +\frac{1}{2^n}(e_n+n)+\frac{1}{2^n}(n)
$$

 and one more:
and one more: