for - paper - Major transitions in sociocultural evolution (2025) - author - Arsham Nejad kourki - criitque of sociocultural systems as ETI
- Last 7 days
-
www.cambridge.org www.cambridge.org
-
-
sociocultural systems typically lack the core conditions required for an ETI, including autonomous reproduction at the group level and the operation of natural selection in the reproductive mode
for - ETI - sociocultural systems as ETI - critique - lack autonomous reproduction at the group level - lack operation of natural selection in the reproductive mode
-
-
www.youtube.com www.youtube.com
-
the teological sin
for - definition - the teological sin - biological systems aren't suppose to have agency!
-
in your latest book that you wrote with your brother brother Raymond Noble living system
for - book - Understanding Living Systems - Denis and Raymond Noble - to - book - Understanding Living Systems - Denis and Raymond Noble - https://hyp.is/M7xm0NeMEfCqc2PC5Mwj2A/dokumen.pub/understanding-living-systems-9781009277365-9781009277396.html
-
-
-
Understanding Living Systems
for - book - Understanding Living Systems -o Denis and Raymond Noble - from - youtube - Denis Noble - interview - We're stuck in a DNA dogma - https://hyp.is/gWe8MteLEfCpKr-k4niKcg/www.youtube.com/watch?v=NAPhBt8VJCM
-
- Dec 2025
-
librarytechnology.org librarytechnology.org
-
https://librarytechnology.org/mergers/<br /> Library technology Mergers
-
-
koha-community.org koha-community.org
-
Koha Library Software The world's first free and open source library system
-
-
www.reddit.com www.reddit.com
-
warburg.sas.ac.uk warburg.sas.ac.uk
-
As Marchand elucidates, it was most likely before his research trip to Rome in autumn 1928 that Warburg had all the material in the then-existent 72 boxes stamped with a number sequence identifying each individual item by its box and its place within the order of items across all boxes (so, for instance, the index card shown in Fig. 2. would be item number 10042 in the overall sequence). This detailed indexing allowed Warburg and Gertrud Bing to assemble a new set of Zettelkästen specifically for the Rome trip without worrying about irredeemably displacing any items from their original locations. These “travelling boxes” were never dismantled as planned, however, and are still part of the Archive today, recognisable by a separate numbering sequence marked in square brackets (e.g. ZK [1]). Although the square-bracketed Zettelkasten sequence now also includes other boxes that were unnumbered at Warburg’s death, the visible difference between the two sequences remains a testimony to the mobility of the Zettelkasten corpus and its role in Warburg’s work on the famous Bilderatlas, a central part of which occurred during the abovementioned Rome trip with Bing.
"travelling boxes" as analog "back up"
-
-
cutlefish.substack.com cutlefish.substack.com
-
This list has received positive feedback. It seems to have struck a nerve. Sending it to coincide with Monday morning to help folks navigate their week.Take care of yourself. Your brain is working overtime—all the time. Practice “radical” recovery.You may spend a lot longer thinking about things than most people. Pace your delivery.If you go deep first, and then simplify…keep in mind that you don’t need to show all of your work.Your default description of (almost) any problem will be too threatening/overwhelming.Do your deepest thinking with co-conspirators (not the people you’re trying to influence).Informal influence is often not formally recognized. Prepare mentally for this.The people you’re trying to influence spend 98% of their day overwhelmed by business as usual.Remember to also do the job you were hired to do (if you don’t you’ll be easier to discount).Seek “quick wins”, but know that most meaningful things will take a while.Some things take ages to materialize. It is discontinuous, not continuous.Make sure to celebrate your wins. They will be few and far between, so savor the moment.The people who support you in private may not be able to support you in public. Accept that.Hack existing power structures—it’s much easier than trying to change them.Consider becoming a formal leader. It’s harder in many ways, but you’ll have more leverage. What’s stopping you?In lieu of being a formal leader, make sure to partner with people who actually “own” the area of change.Watch out for imposing your worldview on people. Have you asked about what people care about?.You’ll need a support network. And not just a venting network. Real support.“Know when to fold ‘em”. Listen to Kenny Rogers The Gambler. Leave on your own terms.Don’t confuse being able to sense/see system dynamics, with being about to “control” them. You can’t.Grapple with your demons, and make sure not to wrap up too much of your identity in change.
-
-
www.youtube.com www.youtube.com
-
FILING PROCEDURES IN BUSINESS 1965 OFFICE MANAGEMENT / SECRETARY TRAINING FILM 62244<br /> by [[Periscope Film]] on YouTube<br /> accessed on 2025-12-03T00:14:39
-
-
Local file Local file
-
THE SCIENCE OF THE FILING ENGINEERThe Simplex Alpabetic Method Is Considered the Most Efficient and Takes Care ofTAverage Requirements - It May Be the 95% File-Complex Methods Also Explained
Butters, Roland W. 1921. “The Science of the Filing Engineer.” Filing & Office Management 6(7): 193–94. https://www.google.com/books/edition/Filing_Office_Management/o1rnAAAAMAAJ?hl=en&gbpv=1&pg=PA193&printsec=frontcover&dq=duplex.
-
Also, many exponents of filing knowledge have saidthat their file is a "fool-proof" one. I believe that youquestion this statement, as the only way to have afile as near perfect as possible, is to have safe andsane ideas and put them into practice; that is whythe Alphabetic file is the 95% file.
Alphabetic filing accounts for 95% of filing systems according to Butters.
-
The reason for this beingin the Complex classification is, as one will tell youwho has operated a Subject File, because a great dealof care must be exercised in not only laying out theproper plan, but working in and cooperating withthose who send matter to be filed, and are constantlyasking for it. The file clerk may think it goes in oneplace, but unless it is carefully marked as to whereit should be filed and then remembered, and possiblyagain classified by card, it is many times found a dif-ficult matter to handle.
-
The next Complex method in order, is the Numeric,which may be divided into three classes, straight num-eric, duplex and decimal. It is safe to say that withthe straight Alphabetic or Geographic, ninety-five per-cent of the cases where an Index is used will be moreefficiently handled by the use of either one of theseMethods, than by the Numeric. However, there aresome cases where there is a great deal of cross refer-ence, thus making the use of the Numeric methodmore advantageous.
This is likely the reason why most commonplacers using index card systems use alphabetic set ups by subject rather than Niklas Luhmann's duplex numeric variation.
-
-
Local file Local file
-
DUPLEX NUMERIC SYSTEM.
-
McCord, James Newton. 1920. A Textbook of Filing. D. Appleton. https://www.google.com/books/edition/A_Textbook_of_Filing/SBowAAAAYAAJ?hl=en&gbpv=0.
-
-
Local file Local file
-
The material filedcan be arranged as the cards would be,so as to bring together all the paperson a given subject.
-
is essential in subject work becausesome subjects are closely related andyet not sufficiently so to be filed to-gether.
The use of the cross reference sheet
A portion of the reason why Luhmann chose a duplex numeric filing system for his zettelkasten.
-
secondary number form of notation be considered in perfect order with-e. g.Administration :1-1-a General1-2-a Officers1-2-b Meetings of officers .This allows for more expansion and iscommonly termed "Duplex Numeric."
The numeric arrangement elim-inates the decimal feature and is used when the number of main divisions is likely to exceed nine, a primary and
This is exactly Niklas Luhamann's zettelkasten numbering system.
-
The object of any system is speedin service, and to obtain this, in sub-ject work, all correspondence on agiven subject must be filed together,regardless of who wrote it or at whattime it was written, so that the historyof everything that has taken place onone subject may be found in one place.
-
Classification of Files of the U. S. ExplosivePlant at Nitro, W. Va.By Miss J. L. Dillard
Dillard, J. L. 1919. “Subject and Classification Filing: Classification of Files in the U.S. Explosive Plant at Nitro, W. Va.” Filing: A Magazine on Indexing & Filing 3(2): 401–3. https://www.google.com/books/edition/Filing/nxFLAAAAYAAJ?hl=en&gbpv=1&pg=PA401&printsec=frontcover&dq=duplex (December 2, 2025).
-
-
Local file Local file
-
ne of the chief drawbacks in using the Alpha-betic and Numeric systems in conjunction with asubject file is that in handling a large amount ofmaterial a great deal of cross referencing has tobe done, causing much extra labor and filling upthe files.
drawbacks of alphabetic and numeric systems with respect to cross referencing
-
utive numbers are assigned to the different sub-jects; if it is necessary to sub-divide these sub-jects, a letter of the alphabet is appended. Thus-Insurance..1 , Auto. Ins... 1-1 , Auto. Fire Ins.-1-1-a.
In the Numeric system of subject filing, consec-
-
A Duplex Numeric system may also be used forSubject filing, which is the using of combinationsof numbers without the decimal limitations. Adash or hyphen being used instead of the decimalmark.
advantages of duplex numeric systems over decimal systems
-
ll correspondence is filed under the correspond-ent's number, unless it relates to branch offices orto a subject relating to some special division ofthe correspondent's business, for which it has beennecessary to assign a separate folder. In this casethey are assigned auxiliary numbers to the mainnumber. This is known as a Duplex Numericsystem of numbering.American Express Co. 52431234 Market St. , Phila., PaNew York City, N. Y.Pittsburgh , Pa.-1-2Rochester , N. Y. -3
-
Lennig, Margaret Antoinette. 1920. Filing Methods: A Text Book on the Filing & Indexing of Commercial & Government Records. https://www.google.com/books/edition/Filing_Methods/vVagv_GyENwC?hl=en&gbpv=0.
-
-
Local file Local file
-
1002. By using the primary and secondary or duplexnumeric system (see §§ 159-163, 432-433) , the primary num-ber can be used to designate the client, each case or matterhandled for that particular client being indicated by thesecondary number, permitting the grouping of the records per-taining to a given client and his affairs in one place.
Luhmann would likely have been aware of duplex numeric systems of filing from legal and governmental filing work. It's not a difficult jump to go from client to subject matter to keep ideas bundled "in one place."
-
Duplex Numeric
Hudders suggests duplex numeric systems for mercantile use, architects, contractors, lawyers' correspondence and for drawings and blueprint filing.
-
620. Should further expansion be required, a third divisioncan be made by suffixing letters of the alphabet in rotation, e.g. :4-3 FIRE INSURANCE4-3a Losses4-3b Agents4-3c Rates4-3d Danger Zones
expanding numeric systems is quite easy
-
615. If the filing is started on a straight numeric basis,with the titles assigned to cover broad groups, it would be pos-sible to expand it to a duplex numeric system either in partor in its entirety if need be.
Numeric systems can be expanded to duplex num.eric systems
-
COMPARISON OF THE DECIMAL ARRANGEMENT WITHTHE DUPLEX NUMERIC ARRANGEMENT ( showing the possibilityof expansion in the latter that is lacking in the decimalclassification )
Notice the one-to-one correspondences between these systems.
There is a sort of artificial lack of extension, but numerically it really doesn't exist mathematically.
-
Hudders, Eugene Russell. 1919. Indexing and Filing: A Manual of Standard Practice. 5th ed. New York: The Ronald Press Company. https://www.google.com/books/edition/Indexing_and_Filing/p_MRAAAAYAAJ?hl=en&gbpv=0.
-
-
Local file Local file
-
Method
-
division can be limited to 26. Although provision for a third subdi-vision can be made, it is not advisable.
The duplex numeric method of filing is designed for use when the number of primary or main subjects exceeds 10 and the second sub-
Specifically note the "is not advisable" portion, particularly with respect to N. Luhmann's practice.
-
DUPLEX NUMERIC SUBJECT FILING
-
- Nov 2025
-
Local file Local file
-
Hunter, Estelle Belle. 1923. Modern Filing Manual. Rochester, NY: Yawman and Erbe Manufacturing Company. https://www.google.com/books/edition/Modern_Filing_Manual/F-lNAQAAMAAJ?hl=en.
-
-
www.wikiwand.com www.wikiwand.com
-
Das gerichtliche Aktenzeichen dient der Kennzeichnung eines Dokuments und geht auf die Aktenordnung (AktO) vom 28. November 1934 und ihre Vorgänger zurück.[4]
The court file number is used to identify a document and goes back to the file regulations (AktO) of November 28, 1934 and its predecessors.
The German "file number" (aktenzeichen) is a unique identification of a file, commonly used in their court system and predecessors as well as file numbers in public administration since at least 1934.
Niklas Luhmann studied law at the University of Freiburg from 1946 to 1949, when he obtained a law degree, before beginning a career in Lüneburg's public administration where he stayed in civil service until 1962. Given this fact, it's very likely that Luhmann had in-depth experience with these sorts of file numbers as location identifiers for files and documents.
We know these numbering methods in public administration date back to as early as Vienna, Austria in the 1770s.
The missing piece now is who/where did Luhmann learn his note taking and excerpting practice from? Alberto Cevolini argues that Niklas Luhmann was unaware of the prior tradition of excerpting, though note taking on index cards or slips had been commonplace in academic circles for quite some time and would have been reasonably commonplace during his student years.
Are there handbooks, guides, or manuals in the early 1900's that detail these sorts of note taking practices?
Perhaps something along the lines of Antonin Sertillanges’ book The Intellectual Life (1921) or Paul Chavigny's Organisation du travail intellectuel: recettes pratiques à l’usage des étudiants de toutes les facultés et de tous les travailleurs (in French) (Delagrave, 1918)?
Further recall that Bruno Winck has linked some of the note taking using index cards to legal studies to Roland Claude's 1961 text:
I checked Chavigny’s book on the BNF site. He insists on the use of index cards (‘fiches’), how to index them, one idea per card but not how to connect between the cards and allow navigation between them.
Mind that it’s written in 1919, in Strasbourg (my hometown) just one year after it returned to France. So between students who used this book and Luhmann in Freiburg it’s not far away. My mother taught me how to use cards for my studies back in 1977, I still have the book where she learn the method, as Law student in Strasbourg “Comment se documenter”, by Roland Claude, 1961. Page 25 describes a way to build secondary index to receive all cards relatives to a topic by their number. Still Luhmann system seems easier to maintain but very near.
<small><cite class='h-cite via'>ᔥ <span class='p-author h-card'> Scott P. Scheper </span> in Scott P. Scheper on Twitter: "The origins of the Zettelkasten's numeric-alpha card addresses seem to derive from Niklas Luhmann's early work as a legal clerk. The filing scheme used is called "Aktenzeichen" - See https://t.co/4mQklgSG5u. cc @ChrisAldrich" / Twitter (<time class='dt-published'>06/28/2022 11:29:18</time>)</cite></small>
Link to: - https://hypothes.is/a/Jlnn3IfSEey_-3uboxHsOA - https://hypothes.is/a/4jtT0FqsEeyXFzP-AuDIAA
-
-
en.wikipedia.org en.wikipedia.org
-
https://en.wikipedia.org/wiki/Soundex
There is a close relationship between the Soundex indexing scheme and the scheme behind the Major System!!!
Tags
- Ingres
- MS SQL Server
- Oracle
- National Archives and Records Administration (NARA)
- Snowflake
- phonetics
- Robert C. Russell
- PostgreSQL
- ClickHouse
- Soundex
- indexing systems
- IBM Db2
- Margaret King Odell
- Donald Knuth
- SQLite
- Major system
- MySQL
- algorithms
- SAP ASE
- phonetic algorithms
- Census Bureau
Annotators
URL
-
-
www.hirensbootcd.org www.hirensbootcd.org
- Oct 2025
-
drphilippahardman.substack.com drphilippahardman.substack.com
-
Why does adding structure to AI workflows work so well? Fundamentally, there are four key reasons. Methodologies like FRAME™:
Why create a structured workflow?
-
-
www.youtube.com www.youtube.com
-
patterns being goal states and uh and not just uh you know, here are the patterns that happen to show up. this is this is an actual goal state that a system that an intelligent system is pursuing
for - quote - patterns are goal states intelligent systems are pursuing - Michael Levin
-
-
www.youtube.com www.youtube.com
-
what happens in living beings uh in living organisms
for - adjacency - TAG - living systems - cell agents - consciousness agent
-
how we can build AI system that are more like biological system
for - building AI systems more like biological systems
-
basically absent or very seldom present in current AI systems
for - comparison - biological vs AI systems
-
for - Michael Levin - Multi Scale Competency Architecture - Hierarchical systems
Summary - Biomimicry - mimicking natural systems for new AI models - human body is a hierarchical system - society is extension of human body and also hierarchical system
-
-
-
"Use Work-Organizers" advertisement, Bookseller & Stationer and Office Equipment Journal, Toronto, October 1920, Vol XXXVI, No. 10, p70.
Photo of a work organizer for indexing/filing on both a desktop as well as within the desk drawer.
-
-
www.biorxiv.org www.biorxiv.org
-
Transparent Peer Review
Download the complete Review Process [PDF] including:
- reviews
- authors' reply
- editorial decisions
-
- Sep 2025
-
bookshelf.vitalsource.com bookshelf.vitalsource.com
-
Real-Time Embedded Systems
A real time embedded system is a small computer built inside a device that does specific jobs and gives results within a fixed time. It is called “real time” because it must respond quickly without delay, like in car airbags, traffic lights, or medical machines. These systems are designed to be fast, reliable, and accurate since even a small delay can cause problems. In simple words, it is a hidden computer inside machines that makes sure they react and work at the right time.
-
- Aug 2025
-
www.youtube.com www.youtube.com
-
the case of pregnancy where you have two immune systems in the same system and not only you have two immune system you have a third immune system which is in the placenta
for - research - pregnancy - 3 immune systems
-
Varela who is very famous in the you know body cog cognition literature he was a biologist and he spent quite some time in into um the immune immune systems
for - adjacency - Verela -immune systems
-
- Jul 2025
-
en.wikipedia.org en.wikipedia.org
-
batesoninstitute.org batesoninstitute.org
-
HOW SYSTEMS GET UNSTUCK
for - stuck systems - how systems get unstuck
-
- Jun 2025
-
www.youtube.com www.youtube.com
-
learning is is a is a free gift from uh the mathematics of networks
for - myth - learning is a property of nervous systems - Michael Levin - salience - high - learning is a property of molecular networks - adjacency - learning - myth - molecular networks - it is a primitive property of molecular networks<br /> - patterns of learning such as habituation, pavlovian response, etc are observable in molecular network - This is a pretty profound claim - learning isn't even a property of the biotic world!
-
- May 2025
-
www.cmarix.com www.cmarix.com
-
The answer most technocrats are leaning towards is vector search technology and Retrieval-Augmented Generation (RAG) models that improve AI experiences. These intelligent search systems are fundamentally changing how users discover information, interact with applications, and receive personalized experiences across industries.
Explore how embedding intelligence transforms Vector Search and RAG (Retrieval-Augmented Generation) models. Learn the key benefits, use cases, and implementation strategies for smarter AI-driven search systems.
-
-
mutabit.com mutabit.com
-
ormato ampliamente utilizado en el intercambio de datos en la web
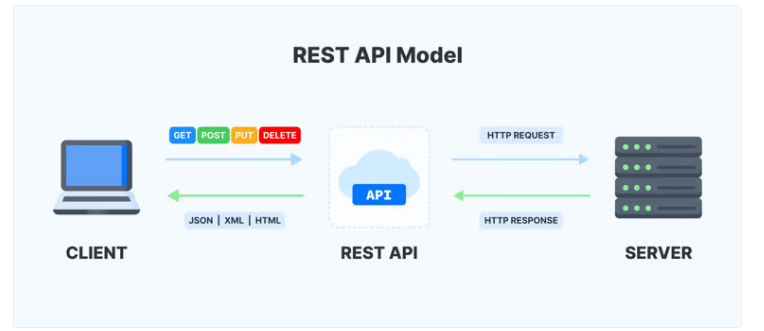
Dicho formato (JSON) también es comúnmente utilizado para el desarrollo de interfaces de programación de aplicaciones (API REST), por ejemplo, en las Bibliotecas universitarias se utiliza usualmente para el vaciado de datos entre los sistemas de información académicos con los ILS para descargar/actualizar los datos de los estudiantes matriculados en una Universidad sin necesidad de hacer cargas por archivo txt, xls, etc.
-
-
www.cmarix.com www.cmarix.com
-
Most legacy apps that aren’t putting efforts into modernization or AI integration are either breaking even, or nearing their demise due to the inability to deliver personalized experiences and use data-driven insights that define market leaders in artificial intelligence legacy systems implementations.
Integrating modern technologies into outdated infrastructures doesn't have to be a challenge. Discover how businesses are successfully integrating AI into legacy systems with NET Core to boost performance, enable predictive insights, and stay ahead in the competitive digital world.
From enhancing data processing to automating workflows, AI and .NET Core offer the perfect synergy to modernize applications without a complete rebuild. 💡
-
- Apr 2025
-
osf.io osf.io
-
framework integrating three therapeutic modes, namely Acceptance and Commitment Therapy (ACT), Outdoor Therapy and Group Therapy. We describe the ACT-GRO(ACT-GroupOutdoor) Framework, its components, rationale behind the proposed Framework and explain how each component enhances the other and can be viewed as a system of systems-a term borrowed from engineering –requiring each system to be autonomous, connected, and diverse, with a common purpose and a commitment to a greater outcome. In the second part, we describe how the three therapeutic modes working in an integrative way meet Baldwin’s criteria of a system of systems. Finally, we
This is an interesting example of applying systems of systems concepts to a form of integrated therapy. By maintaining the same rigorous requirements for characterization as a system of systems, a framework emerges which can be applied to other integrated systems.
-
-
www.redbook.io www.redbook.io
Tags
Annotators
URL
-
- Mar 2025
-
peeragogy.org peeragogy.org
-
for - from - Christina Bowens - Network Coordination Commons meeting - Dialogue on Convening Systems: What does it take? What does it look like on the ground?
-
-
web.cvent.com web.cvent.com
-
Project Dandelion: Women, Food, and the Climate Future
for - program event selection - 2025 - April 3 - 1-4pm GMT - Skoll World Forum - Project Dandelion: Women, Food and the Climate Future - Agrosphere Systems - relevant to
-
-
en.wikipedia.org en.wikipedia.org
-
cross reference Universal Decimal Classification, Dewey Decimal Classification
-
-
www.taylorfrancis.com www.taylorfrancis.com
-
Commons Economies in ActionMutualizing Urban Provisioning Systems
for - book - Sacred civics - ch 16 - Commons Economies in Action - Mutualizing Urban Provisioning Systems - Michel Bauwens - Jose Ramos - Ron Kranjc
-
-
www.lucsus.lu.se www.lucsus.lu.se
-
for - Christine Wamsler - Lund University - homepage - from - youtube - Mindfulness World Community - Awareness, Care and Sustainability for Our Earth - https://hyp.is/GCUJ1APHEfCcr_vvv3lAFw/www.youtube.com/watch?v=CTUc_0GroGM
-
to - paper - An Interdisciplinary Model to Foster Existential Resilience and Transformation
-
to - paper - Engaging high-income earners in climate action : Policy insights from survey experiments
- for Deep Humanity Wealth 2 Wellth program
- https://hyp.is/MIc0DgPKEfC_Z5v_n8P8mA/www.sciencedirect.com/science/article/pii/S0921800924002842
-
to - paper - Revolutionising sustainability leadership and education : addressing the human dimension to support flourishing, culture and system transformation
- for - LCE leadership academy
- https://hyp.is/nLBHtAPLEfCvUUNZrc_uqw/link.springer.com/article/10.1007/s10584-023-03636-8
-
to - The System Within : Addressing the inner dimensions of sustainability and systems change
- to - paper - Transformative Climate Resilience Education for Children and Youth: From Climate Anxiety to Resilience, Creativity and Regeneration, Literature review conducted for the ERASMUS+ Project 2023-1-SE01-KA220-SCH-000158705
- for - SRG/TPF/LCE ward-level afterschool outreach program but it's currently a dead link and inaccessible
- to - IMAGINE sustainability : integrated inner-outer transformation in research, education and practice
- for - Deep Humanity open source praxis
- Human Interior Transformation (HIT) and
- Social Exterior Transformation (SET) //
- https://hyp.is/5_GsSAPNEfC82DMDillDTw/link.springer.com/article/10.1007/s11625-023-01368-3
research areas - sustainable cities - collaborative governance - city-citizen collaboration - citizen participation - sustainability and wellbeing - sustainability transformation - inner development goals - inner transformation - inner transition - existential sustainability
-
Tags
- from - youtube - Mindfulness World Community - Awareness, Care and Sustainability for Our Earth
- for - Deep Humanity Wealth 2 Wellth program
- to - The System Within : Addressing the inner dimensions of sustainability and systems change
- to - paper - Transformative Climate Resilience Education for Children and Youth: From Climate Anxiety to Resilience, Creativity and Regeneration, Literature review conducted for the ERASMUS+ Project 2023-1-SE01-KA220-SCH-000158705
- to - IMAGINE sustainability : integrated inner-outer transformation in research, education and practice
- for - LCE leadership academy
- for - SRG/TPF/LCE ward-level afterschool outreach program but it's currently a dead link and inaccessible
- to - paper - Engaging high-income earners in climate action : Policy insights from survey experiments
- to - paper - Revolutionising sustainability leadership and education : addressing the human dimension to support flourishing, culture and system transformation
- to - paper - An Interdisciplinary Model to Foster Existential Resilience and Transformation
- Christine Wamsler - Lund University - homepage
- Christine Wamsler - research areas
Annotators
URL
-
-
www.clubofrome.org www.clubofrome.org
-
for - from - Christine Wamsler - homepage - Lund University - https://hyp.is/XgmNsgPHEfCBOPszkHcE3Q/www.lucsus.lu.se/christine-wamsler - sustainability - bridging inner and outer transformation - Club of Rome report - The system within - addressing the inner dimensions of sustainability and system transformation - Earth4all report - The system within - addressing the inner dimensions of sustainability and systems transformation - Deep Humanity - interior and exterior transformation
Tags
- Earth4all report - The system within - addressing the inner dimensions of sustainability and systems transformation
- Club of Rome report - The system within - addressing the inner dimensions of sustainability and system transformation
- sustainability - bridging inner and outer transformation
- from - Christine Wamsler - homepage - Lund University
- eep Humanity - interior and exterior transformation
Annotators
URL
-
- Feb 2025
-
htmx.org htmx.org
-
Here, the “hypermedia controls” are encoded in a links property on the account object.
Véase el comentario extraído de de REST APIs must be hypertext-driven en las notas de lectura en mi bliki.
Tags
Annotators
URL
-
-
-
for - Tim - Social Systems Lab
Tags
Annotators
URL
-
-
srsergiorodriguez.github.io srsergiorodriguez.github.io
-
El aglutinante es que tales elementos están pensados y organizados desde de las lógicas del diseño web y la programación.
La web en cambio me parece incidental para los ensayos interactivos y muchos de ellos existieron antes de la web, desde los tiempos del Dynabook de Kay, Ingalls y Golberg hasta el Hypercard o el Dynamicland en dicha tradición.
A contracorriente, suelo pensar el diseño web y la web en general no cómo una plataforma de desarrollo sino como un "exportation target", que ahora se vuelve más multilingüe, más allá de Javascript y todas sus falencias gracias a posibilidades como las abiertas con los Sistemas Hipermediales.
-
-
srsergiorodriguez.github.io srsergiorodriguez.github.io
-
Interactivo 7. Un mapa de vectores que representa la semántica distribucional de los artículos publicados hasta el Vol. 8 de la Revista de Humanidades Digitales
Y también existe un interés por las reflexiones al respecto del acceso, la democratización y la accesibilidad de los archivos, y en general una postura a favor del software y la ciencia abierta.
Aunque a este nivel de zoom o alguno cercano hacia afuera (zoom out) no se alcanza a ver dicha postura en las palabras que el mapa muestra.
Muy interesantes los interactivos a lo largo del texto. Su dependencia de JavaScript, también para los textos acompañantes hace difícil anotarlos con Hypothesis. Me pregunto si herramientas hipérmediales como HTMX, Data Star e incluso AlpineJS permitirían que cierta parte del texto sea estática y embebida en la salida HTML, así corresponda a visualizaciones dinámicas que se presentan progresivamente.
-
- Jan 2025
-
lepiter.io lepiter.io
-
At the same time, it is the only environment today in which to learn and practice Moldable Development.
Esto ya no es cierto. Sistemas como Clerk han adoptado explícitamente el término amoldable para describir la visión, citando a Tudor y su grupo.
En Grafoscopio, nos hemos venido decantando por Sistemas Maleables, pues siento que describe mejor nuestra intención distinta no de "iniciar una conversación" (entre desarrolladores) como afirma Tudor, sino de enmarcarnos en una conversación más antigua, diversa y amplia, que por ejemplo recoge ideas de Maturana y Varela (autopoiesis), Freire (alfabetismos críticos), Kay (Dynabook), la comunidad de Pharo, la de GToolkit, Wenger (comunidades de prácticas) y las propias en diálogo con ellas (infraestructuras de bolsillo, computación convivial) etc.
-
ndeed, as we can only perceive details related to a software system through tools, it follows that the tools are essential to the act of programming. At the same time, because software is highly contextual, for tools to be effective they also have to be contextual. The above examples are all quite different. In fact, each could be considered as a separate vertical in the software engineering tooling space. Yet, they were all expressed uniformly in the same environment. This shows that these tools are not distinct and that they can be combined and customized arbitrarily. There is just a fluid environment. We do not go to tools. Tools come to us. And we can make them come to us in our terms, in our context. That's the premise of Moldable Development.
-
-
www.cambridge.org www.cambridge.org
-
system reflexivity
for - definition - system reflexivity (Moore et al., 2018) - the capacity to see the complexity and mobilize the agency in a system, while deeply engaging with diversity across multiple scales - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
-
individual reflexivity is rarely traced through to a collective influence on the broader transdisciplinary research process
for - adjacency - individual reflexivity is rarely traced to a collective influence - Indyweb provenance - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
adjacency - between - individual reflexivity is rarely traced to a collective influence - Indyweb provenance - adjacency relationship - Indyweb provenance can allow granular tracing of individual contributions to collective knowledge work - so can assist in the use of reflexivity in transdisciplinary work
-
Reflexivity has been explored on a collective societal level, for example through Ulrich Beck's work on reflexive modernization wherein the unintended consequences of simple modernity motivate a reflexive turn across society, including to science itself: ‘science itself is deconstructed by means of science’
for - further research - Ulrich Beck's research on unintended consequences of simple modernity - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
-
In the context of transformative transdisciplinary research, such reflexive processes are meant to open-up epistemic and solution spaces that elevate marginalized perspectives and challenge the status quo.
for - adjacency - reflexive processes elevate marginalized perspectives and challenge status quo - diversity of Indyweb perspectival knowing - mitigates progress traps that emerge from myopism - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
-
avigating the diverse and sometimes conflicting perspectives of researchers and participants in transdisciplinary processes raises challenges
for - adjacency - challenges of harmonizing multiple perspectives - SRG complexity mapping - Deep Humanity - embedded in Indyweb - intrinsic perspectival knowing - facilitates high resolution perspectival complementarity - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
-
Transdisciplinary sustainability science is increasingly applied to study transformative change. Yet, transdisciplinary research involves diverse actors who hold contrasting and sometimes conflicting perspectives and worldviews. Reflexivity is cited as a crucial capacity for navigating the resulting challenges
for - adjacency - reflexivity - tool for transdisciplinary research - indyweb - people-centered interpersonal information architecture - mindplex - concept spaces - perspectival knowing - life situatedness - SRG transdisciplinary complexity mapping tool - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
adjacency - between - reflexivity - tool for transdisciplinary research - indyweb - people-centered, interpersonal information architecture - mindplex - concept space - perspectival knowing - life situatedness - SRG transdisciplinary complexity mapping tool - adjacency relationship - This paper is interesting from the perspective of development of the Indyweb because there, - the people-centered, interpersonal information architecture intrinsically explicates perspectival knowing and life-situatedness - Indyweb can embed an affordance that is a meta function applied to an indyvidual's mindplex that - surfaces and aspectualizes the perspective and worldview salient to the research - The granular information that embeds an indyvidual's perspectives and worldviews is already there in the indyvidual's rich mindplex
-
as crucial dimensions are left unacknowledged
for - in other words - remain implicit instead of made explicit - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
-
for - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
Tags
- paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
- definition - system reflexivity (Moore et al., 2018) - the capacity to see the complexity and mobilize the agency in a system, while deeply engaging with diversity across multiple scales - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
- adjacency - reflexive processes elevate marginalized perspectives and challenge status quo - diversity of Indyweb perspectival knowing - mitigates progress traps that emerge from myopism - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
- adjacency - individual reflexivity is rarely traced to a collective influence - Indyweb provenance - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
- adjacency - challenges of harmonizing multiple perspectives - SRG complexity mapping - Deep Humanity - embedded in Indyweb - intrinsic perspectival knowing - facilitates high resolution perspectival complementarity - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
- further research - Ulrich Beck's research on unintended consequences of simple modernity - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
- adjacency - reflexivity - tool for transdisciplinary research - indyweb - people-centered interpersonal information architecture - mindplex - concept spaces - perspectival knowing - life situatedness - SRG transdisciplinary complexity mapping tool - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
- in other words - remain implicit instead of made explicit - SOURCE - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10
Annotators
URL
-
-
www.linkedin.com www.linkedin.com
-
New paper! For those of you just starting out in transdisciplinary research, or for those of you that have been doing it a long time and engaging in reflexive practices,
for - adjacency - post - LinkedIn - new paper - reflexivity in transdisciplinary research - Indyweb research - to - paper - Reflexivity as a transformative capacity for sustainability science: introducing a critical systems approach - Lazurko et al. - 2025, Jan 10 - https://hyp.is/SXryuNSYEe-1zcu9-Y2ncA/www.cambridge.org/core/journals/global-sustainability/article/reflexivity-as-a-transformative-capacity-for-sustainability-science-introducing-a-critical-systems-approach/D6978EE9FF6C9B7DBB36212C2BB0B865
-
-
www.youtube.com www.youtube.com
-
lots of homes right along the ocean completely torched so the question is why didn't they have hoses that they could put in the ocean and pump seawat onto the roofs and structures to keep the Cinders from uh setting the place light and burning It To The Ground just a thought
for - climate crisis - forest fires - home protection - outside rooftop sprinkler systems - SOURCE - Youtube - climate crisis - 2025 Los Angeles fires - The Catastrophic Climate Driven Conflagaration in Los Angeles - Paul Beckwith - 2025, Jan 10
// - COMMENT - Paul brings up a very good point. There is an existing low cost innovation that was pioneered and successfully deployed in Canada that could have prevented the destruction of many of the buildings that were destroyed, namely - rooftop sprinkler systems - There are many rooftop sprinker systems available now. They should actually be mandated into law to have one in high risk fire areas. - https://search.brave.com/search?q=canada+forest+fire+prevention+rooftop+sprinkler+system&source=desktop&summary=1&conversation=375a9992d731deff34143a
Tags
- climate crisis - forest fires - home protection - outside rooftop sprinkler systems - SOURCE - Youtube - climate crisis - 2025 Los Angeles fires - The Catastrophic Climate Driven Conflagaration in Los Angeles - Paul Beckwith - 2025, Jan 10
- - rooftop fire sprinkler systems would have saved many building - SOURCE - Youtube - climate crisis - 2025 Los Angeles fires - The Catastrophic Climate Driven Conflagaration in Los Angeles - Paul Beckwith - 2025, Jan 10s -
Annotators
URL
-
-
futureoffood.org futureoffood.org
-
for - report - climate crisis - food system transformation - Public climate finance for food systems transformation - Global Alliance for the Future of Food - 2024, Nov - from - post - LinkedIn - Jonathan Foley - This is very, very important - stats - 2.5% climate funding for food system that contributes 30% of global climate emissions - 2025, Jan 3 - https://hyp.is/zKE7vsqkEe-RFB8co7Pdqw/www.linkedin.com/posts/jonathan-foley-182808b9_foodsystemeconomicscommission-cop29-climatefinance-activity-7281009061003706369-P1b0/ - TPC network - motivation
Tags
- report - climate crisis - food system transformation - Public climate finance for food systems transformation - Global Alliance for the Future of Food - 2024, Nov
- TPC network - motivation
- from - post - LinkedIn - Jonathan Foley - This is very, very important - stats - 2.5% climate funding for food system that contributes 30% of global climate emissions - 2025, Jan 3
Annotators
URL
-
-
www.linkedin.com www.linkedin.com
-
While the food system contributes about 22-34% of the world’s greenhouse gases — it only gets about 2.5-3% of the climate funding.
for - stats - climate crisis - funding - food system - contributes 30% of global emissions - receives 2.5% climate funding - only 1.5% of the 2.5% goes to sustainable food systems - source - Public climate finance for food systems transformation - Global Alliance for the Future of Food - 2024, Nov - reposted on LinkedIn by Jonathan Foley - to - Public climate finance for food systems transformation - Global Alliance for the Future of Food - 2024, Nov - https://hyp.is/E3p2hsqlEe-tG0ezHCPriw/futureoffood.org/wp-content/uploads/2024/11/ga_climatefinancereport_2024.pdf - TPC network - motivation
Tags
- TPC network - motivation
- to - Public climate finance for food systems transformation - Global Alliance for the Future of Food - 2024, Nov
- stats - climate crisis - funding - food system - contributes 30% of global emissions - receives 2.5% climate funding - only 1.5% of the 2.5% goes to sustainable food systems - source - Public climate finance for food systems transformation - Global Alliance for the Future of Food - 2024, Nov - reposted on LinkedIn by Jonathan Foley
Annotators
URL
-
- Dec 2024
-
www.reddit.com www.reddit.com
-
The Advance also uses a mechanism which rotates at 2x the speed of some of the others with the stated intent of being geared towards western alphabet writing, as opposed to Japanese / Asian logograpic writing systems where the user picks up their pencil tip more frequently.
-
-
www.showwcase.com www.showwcase.com
-
You must ensure a clear set of information to be added in the design, consistency is the prime requirement for the branding.
Creating scalable design systems ensures consistency and efficiency in product development. From establishing a robust design foundation to incorporating component libraries and collaboration tools, scalability is key to long-term growth. Enhance your design workflows with modularity, flexibility, and team alignment to future-proof your systems. Perfect for startups and enterprises aiming to deliver seamless user experiences.
-
-
www.linkedin.com www.linkedin.com
-
Drawing on ancient wisdom can help co-create systems that prioritise ecological reverence and community over individualistic domination
for - post - LinkedIn - How Chinese Philosophy Offers Pathways to a Regenerative Future - Man Fang - Post Growth Institute - to - Medium - Rediscovering Harmony: How Chinese Philosophy Offers Pathways to a Regenerative Future - By foregrounding relationships — between individuals, communities, and the natural world — we can build systems that prioritize wellbeing and resilience - Post Growth Institute - Man Fang
to - Medium - Rediscovering Harmony: How Chinese Philosophy Offers Pathways to a Regenerative Future - By foregrounding relationships — between individuals, communities, and the natural world — we can build systems that prioritize wellbeing and resilience - Post Growth Institute - Man Fang - https://hyp.is/a2HCSrlTEe-um4thfDGo-A/medium.com/postgrowth/rediscovering-harmony-how-chinese-philosophy-offers-pathways-to-a-regenerative-future-07a097b237a0
Tags
- post - LinkedIn - How Chinese Philosophy Offers Pathways to a Regenerative Future - Man Fang - Post Growth Institute
- to - Medium - Rediscovering Harmony: How Chinese Philosophy Offers Pathways to a Regenerative Future - By foregrounding relationships — between individuals, communities, and the natural world — we can build systems that prioritize wellbeing and resilience - Post Growth Institute - Man Fang
Annotators
URL
-
-
www.cmarix.com www.cmarix.com
-
Instead of using the conventional 4-digit PIN, you can select a 6-digit code if you’d like even more security. Apple Pay uses tokenization to secure your credit card information, and like other well-known electronic wallets, it doesn’t save credit card information on your device.
Discover the top NFC payment apps driving seamless contactless transactions. Learn how NFC technology simplifies mobile payments, empowering businesses and users with enhanced security and convenience. Explore features of leading apps like Apple Pay, Google Pay, and Samsung Pay. Perfect for businesses looking to adopt NFC payment systems or individuals seeking secure, fast payment solutions.
-
-
theconversation.com theconversation.com
Tags
- COP29
- date:: 2024-12-09
- Trump administration
- by: Laurie Laybourn
- by: James Dyke
- The climate-sovereign debt doom loop: what does the literature suggest?
- Strategic Climate Risks Initiative
- Derailment risk: A systems analysis that identifies risks which could derail the sustainability transition
Annotators
URL
-
-
www.youtube.com www.youtube.com
-
And for for someone like me who was born in this in the country of the US, who came into life as a white presenting woman, it is the work of my life to entirely and utterly work to dismantle oppressive systems simultaneously while I'm actually working to shift my consciousness about how I respond
for - key insight - challenging ourselves for authentic, transformative change - inner and outer work to dismantle oppressive, entrenched systems - Post Capitalist Philanthropy Webinar 1 - Alnoor Ladha - Lynn Murphy - 2023
-
-
www.biorxiv.org www.biorxiv.org
-
Transparent Peer Review
Download the complete Review Process [PDF] including:
- reviews
- authors' reply
- editorial decisions
-
- Nov 2024
-
Local file Local fileLayout 11
-
In the 1950s and 1960s, information retrieval (IR) theorists drew a distinction between“document retrieval systems” and “fact retrieval systems.” The former, were intendedto retrieve, in response to a user’s query, all documents that might contain informationpertinent to answering that query, while the latter were to lead the user directly tospecific pieces of information – facts – embedded within the documents being searchedthat would answer his or her question. The idea of information analysis clearlyprovided the theoretical impetus for fact retrieval (aka question-answering) systems
-
-
analogoffice.net analogoffice.net
-
"How To" Directory by [[Anna Havron]]
-
-
en.wikipedia.org en.wikipedia.org
-
Stafford Beer coined and frequently used the term POSIWID (the purpose of a system is what it does) to refer to the commonly observed phenomenon that the de facto purpose of a system is often at odds with its official purpose
the purpose of a system is a what it does, POSIWID, Stafford Beer 2001. Used a starting point for understanding a system as opposed to intention, bias in expectations, moral judgment, and lacking context knowledge.
Tags
Annotators
URL
-
- Oct 2024
-
Local file Local file
-
System
card system ⇒ system theory
In the early 1900s it was very common, especially in English speaking countries to call these note taking/paper database systems "card systems". Is it a wonder then that they may have helped to create "systems theory"?
In particular, look at Niklas Luhmann's work as well as Ross Ashby.
Example of a fleeting note triggered by a single word in a context, but with thoughts not relating at all to the specifics of the particular work.
-
- Sep 2024
-
coevolving.com coevolving.com
-
coevolving.com coevolving.com
-
www.baldurbjarnason.com www.baldurbjarnason.com
-
glorious rant by Baldur Bjarnason, but not much surprisal here. As with other stuff, albeit agile scrum, getting things done, and any of the pitched perfect ways to make notes, whenever the process becomes the thing rather than a tool in the hand of an knowledge artisan stuff is useless and boring.
It's about output, not in units or volume, but in quality. Needing to know why your are making these notes, and weaving your network of meaning.
The people who do things with their system usually don't talk about it much. I've done it on occasion and am happy to share and show how/why I do things, but never with the intention to convince another to do the same or similar.
-
-
dl.acm.org dl.acm.org
-
Therefore, similar to Ribes et al. in their study of domain [113], the epistemic positions we propose aim to provide conceptual tools for reasoning about different styles of organizing creativity-oriented research practices in HCI.
David Ribes' work explores the definition of domain in computing and data science; offers insight into how studying domains helps organize computational systems.
-
-
www.thelancet.com www.thelancet.com
-
Our estimated safe ESB is that around 50–60% of global land surface should be in largely intact, natural condition to halt species extinction, secure biosphere contributions to climate regulation, and stabilise regional water cycles.
for - stats - earth system boundary - biodiversity - intact natural systems - 50 to 60% global land need to be intact
-
The amount of intact natural land as of 2018 was around 15% below this ESB, but could be increased through restoring degraded ecosystems or previously converted ecosystems,102,103,106102.Strassburg, BBN ∙ Iribarrem, A ∙ Beyer, HL ∙ et al.Global priority areas for ecosystem restorationNature. 2020; 586:724-729CrossrefScopus (536)PubMedGoogle Scholar103.Jung, M ∙ Arnell, A ∙ de Lamo, X ∙ et al.Areas of global importance for conserving terrestrial biodiversity, carbon and waterNat Ecol Evol. 2021; 5:1499-1509CrossrefScopus (162)PubMedGoogle Scholar106.Wolff, S ∙ Schrammeijer, EA ∙ Schulp, CJE ∙ et al.Meeting global land restoration and protection targets: what would the world look like in 2050?Glob Environ Change. 2018; 52:259-272CrossrefScopus (72)Google Scholar with conservation efforts distributed across all ecoregions.
for - stats - earth system boundary - biodiversity - intact natural systems - 15% below ESB in 2018
-
-
www.centreforpublicimpact.org www.centreforpublicimpact.org
- Aug 2024
-
www.youtube.com www.youtube.com
-
Maybe a democracy can work, if it's voting system works well enough.
Tags
Annotators
URL
-
-
frontside.com frontside.com
-
Designers want every part of the app interface and all the elements to have the same look and feel, and design tokens were created to help them achieve that outcome.
Design tokens are platform-agnostic and are the first layer of design decisions in a design system.
-
-
www.youtube.com www.youtube.com
-
The song's criticism on mass media is mainly related to sensationalism.
"Good" things are usually not sensational. They do not demand attention, hence why the code of known/unknown based on selectors for attention filters it out.
Reference Hans-Georg Moeller's explanations of Luhmann's mass media theory based on functionally differentiated systems theory.
Can also compare to Simone Weil's thoughts on collectives and opinion; organizations (thus most part of mass media) should not be allowed to form opinions as this is an act of the intellect, only residing in the individual. Opinion of any form meant to spread lies or parts of the truth rather than the whole truth should be disallowed according to her because truth is a foundational, even the most sacred, need for the soul.
People must be protected against misinformation.
-
-
-
Alternate systems for helping to thin out typewriter collections:
Designer William Morris' weighing system:
“Have nothing in your houses that you do not know to be useful or believe to be beautiful.”
I once had a collector friend who loved standard typewriters, so his weighing system was as follows:<br /> - If it weighs over 25 pounds, keep it<br /> - If it weighs less than 25 pounds, sell it off
And naturally, minimalist Marie Kondo's system:<br /> - Does it spark joy?
Joe Van Cleave also had another video for creating a minimal collection based on categories of typewriter which may also be useful for some: https://www.youtube.com/watch?v=0Ej6kd1FsnE
-
-
-
Solutions or systems that are created uh to solve problems
for - question - neuroscience - creating neuroscience-based systems for solving problems
-
- Jul 2024
-
www.biorxiv.org www.biorxiv.org
-
Transparent Peer Review
Download the complete Review Process [PDF] including:
- reviews
- authors' reply
- editorial decisions
-
-
www.cecan.ac.uk www.cecan.ac.uk
-
Centre for the Evaluation of Complexity Across the Nexus
for - complexity - evaluation - from - paper - Building a system-based Theory of Change using Participatory Systems Mapping
-
-
journals.sagepub.com journals.sagepub.com
-
for - paper review - building a system-based Theory of Change using Participatory Systems Mapping - participatory systems mapping - SRG / Indyweb dev - system mapping - participatory approach
summary - I'm reviewing this paper because the title seems salient for the development of our own participatory Stop Reset Go system mapping tool within Indyweb ecosystem. - The building of - a systems-based Theory of Change using - Participatory Systems Mapping - is salient to our own project and aligns to it with different language: - Theory of Change with uses theory to perform an evaluation and propose an intervention - The Stop Reset Go framework focuses on the specific type of process called "improvement", or - transforming a process to make it "better" in some way
to - Indyweb project info page - https://hyp.is/RRevQk0UEe-xwP-i8Ywwqg/opencollective.com/open-learning-commons/projects/indy-learning-commons
-
-
opencollective.com opencollective.com
-
Indy Learning Commons
for - Indyweb information page - Open Collective Indyweb
from - Paper Review - Participatory Systems Mapping - https://hyp.is/FSRodE0QEe-Z26cIILK6sw/journals.sagepub.com/doi/10.1177/1356389020980493
-
-
-
A critique on the Mass Media... The problem is that they want the Mass Media system to operate on the code of "True/False" rather than "Known/Unknown"... But if it were to be so, it would not be Mass Media anymore, but rather the Science System.
For Mass Media to be Mass Media it needs to be concerned with selection and filtering, to condense and make known, not to present "all the facts". Sure, they need to be concerned with truth to a certain degree, but it's not the primary priority.
This is a reflection based on my knowledge of Luhmann's theory of society as functionally differentiated systems; as explained by Hans-Georg Moeller (Carefree Wandering) on YouTube.
-
- Jun 2024
-
www.youtube.com www.youtube.com
-
Claude Shannon Ultimate Machine
Could this be the end result of artificial intelligence?
cross reference: - Niklas Luhmann's jokerzettel - War Games (1983) and "Joshua" (WOPR)
-
-
niklas-luhmann-archiv.de niklas-luhmann-archiv.de
-
https://niklas-luhmann-archiv.de/bestand/literatur/item/shannon_weaver_1949_communication
Overlap of Claude Shannon and Niklas Luhmann
-
-
coevolving.com coevolving.com
-
Creating building systems in the present sense is not enough. We need a new, more subtle kind of building system
-
A generating system, in this sense, may have a very simple kit of parts, and very simple rules.
-
The formal systems of mathematics are systems in this sense. The parts numbers, variables, and signs like + and =. The rules specify ways of combining three parts to form expressions, and ways of forming expressions from other expressions, and ways of forming true sentences from expressions, and ways of forming true sentences from other true sentences. The combinations of parts, generated by such a system, are the true sentences, hence theorems, of mathematics. Any combination of parts which is not formed according to the rules is either meaningless or false
-
computation of such interrelational, complex behaviour-based systems
-
complex systems of interactions and reciprocities
- complex systems
- interactions and reciprocities
-
-
systems may come to necessitate their own propagation, he suggests, when we use them.
-
Almost every ‘system as a whole’ is generated by a ‘generating system’. If we wish to make things which function as ‘wholes’ we shall have to invent generating systems to create them.
Alexander 2011, p. 59; Alexander 1968, p. 605
-
-
-
www.bitsofwonder.co www.bitsofwonder.co
-
coevolving.com coevolving.com
-
-
how do we sort of cultivate an 00:40:56 intuition for complex systems right for those second third nth order effects
for - question - Entangled Worlds podcast - How do we cultivate intuition for complex systems - to access those higher order effects? - answer - Nora Bateson - practice everywhere
-
-
www.youtube.com www.youtube.com
-
(~0:45)
Justin mentions that a better way to think about learning is in systems rather than techniques. This is true for virtually anything. Tips & Tricks don't get you anywhere, it is the systems which bring you massive improvements because they have components all working together to achieve one goal or a set of goals.
Any good system has these components working together seamlessly, creating something emergent; worth more than the sum of its parts.
-
-
www.youtube.com www.youtube.com
-
The Fastest Way To Achieve Literally Anything (You'll Never Feel Lost Again)
Tags
Annotators
URL
-
-
www.belfercenter.org www.belfercenter.org
-
TensionThe ability to see like a data structure afforded us the technology we have today. But it was built for and within a set of societal systems—and stories—that can’t cope with nebulosity. Worse still is the transitional era we’ve entered, in which overwhelming complexity leads more and more people to believe in nothing. That way lies madness. Seeing is a choice, and we need to reclaim that choice. However, we need to see things and do things differently, and build sociotechnical systems that embody this difference.This is best seen through a small example. In our jobs, many of us deal with interpersonal dynamics that sometimes overwhelm the rules. The rules are still there—those that the company operates by and laws that it follows—meaning there are limits to how those interpersonal dynamics can play out. But those rules are rigid and bureaucratic, and most of the time they are irrelevant to what you’re dealing with. People learn to work with and around the rules rather than follow them to the letter. Some of these might be deliberate hacks, ones that are known, and passed down, by an organization’s workers. A work-to-rule strike, or quiet quitting for that matter, is effective at slowing a company to a halt because work is never as routine as schedules, processes, leadership principles, or any other codified rules might allow management to believe.The tension we face is that on an everyday basis, we want things to be simple and certain. But that means ignoring the messiness of reality. And when we delegate that simplicity and certainty to systems—either to institutions or increasingly to software—they feel impersonal and oppressive. People used to say that they felt like large institutions were treating them like a number. For decades, we have literally been numbers in government and corporate data structures. BreakdownAs historian Jill Lepore wrote, we used to be in a world of mystery. Then we began to understand those mysteries and use science to turn them into facts. And then we quantified and operationalized those facts through numbers. We’re currently in a world of data—overwhelming, human-incomprehensible amounts of data—that we use to make predictions even though that data isn’t enough to fully grapple with the complexity of reality.How do we move past this era of breakdown? It’s not by eschewing technology. We need our complex socio-technical systems. We need mental models to make sense of the complexities of our world. But we also need to understand and accept their inherent imperfections. We need to make sure we’re avoiding static and biased patterns—of the sort that a state functionary or a rigid algorithm might produce—while leaving room for the messiness inherent in human interactions. Chapman calls this balance “fluidity,” where society (and really, the tech we use every day) gives us the disparate things we need to be happy while also enabling the complex global society we have today.
-
However, it’s not this particular system that failed but rather the mode of society that depends on rigid systems to function. Replacing one rigid system with another won’t work.
-
The complexity of society today, and the failure of rigid systems to cope, is scary to many. Nobody’s in charge of, or could possibly even understand, all these complex technological systems that now run our global society.
-
Now, nebulosity, complexity, and the breakdown of these systems is all around for everyone to see.
-
The challenge with previous generations of tech—and the engineers who built them—is that they got stuck in the rigidity of systems.
-
To boost its search engine rankings, Thai Food Near Me, a New York City restaurant, is named after a search term commonly used by potential customers. It’s a data layer on top of reality. And the problems get worse when the relative importance of the data and reality flip. Is it more important to make a restaurant’s food taste better, or just more Instagrammable? People are already working to exploit the data structures and algorithms that govern our world. Amazon drivers hang smartphones in trees to trick the system. Songwriters put their catchy choruses near the beginning to exploit Spotify’s algorithms. And podcasters deliberately mispronounce words because people comment with corrections and those comments count as “engagement” to the algorithms.These hacks are fundamentally about the breakdown of “the system.” (We’re not suggesting that there’s a single system that governs society but rather a mess of systems that interact and overlap in our lives and are more or less relevant in particular contexts.)
-
- May 2024
-
www.biorxiv.org www.biorxiv.org
-
Transparent Peer Review
Download the complete Review Process [PDF] including:
- reviews
- authors' reply
- editorial decisions
-
-
www.researchgate.net www.researchgate.net
-
A major implication of the lack of effective training is thatstudents are often left to struggle through disjointed, flawedlearning experiences while using LMSs during a class.
lack of faculty training - less than stellar student experiences in LMS systems
-
-
www.univ.ox.ac.uk www.univ.ox.ac.uk
-
for - critique of - Gene Centricity - Denis Noble
from - youtube -Evolution 2 Podcast Interview - Denis Noble - Book - Understanding Living Systems - https://hyp.is/-EuWvBYHEe-t9xtn9h1dhA/docdrop.org/video/oHZI1zZ_BhY/
-
-
www.nature.com www.nature.com
-
for - recombination of proteins in higher level proteins - from - youtube - Evolution 2 podcast interview - book - Understanding Living Systems - Denis Noble - Ray Noble
from - youtube - Evolution 2 podcast interview - book - Understanding Living Systems - Denis Noble - Ray Noble - https://hyp.is/OttWABYFEe--gLNFyeNyTw/docdrop.org/video/oHZI1zZ_BhY/
-
-
-
we also challenge in the book The Very concept of selfishness itself
for - book - Understanding living systems - challenging selfishness - critique - of Richard Dawkins' Selfish Gene
- Ray Noble points out a contradiction in Richard Dawkin's use of the word selfish in his "Selfish gene".
- Unless there is purposefulness, choice and agency, there cannot be any concept of selfishness
- Ray Noble points out a contradiction in Richard Dawkin's use of the word selfish in his "Selfish gene".
-
for - Denis Noble - Ready Noble - evolutionary biology - critique of Richard Dawkins Selfish Gene theory - critique of gene centrism - book - Understanding Living Systems - human agency
summary - In this informative interview, brothers Denis and Ray Noble discuss their new book - Understanding Living Systems, and - dispel the 70 year old narrative of Gene centrism and the selfish gene as determining the high level behaviour of living organisms
-
-
english.tau.ac.il english.tau.ac.il
-
for - Oded Rechavi - neurobiology - gene centrism - critique - from - youtube podcast interview - book - Understanding Living Systems - Ray Noble - Denis Noble
summary - Rechavi performed experiments with C Elegan and demonstrated that it possesses a type of neuron that - produces RNA that in response to elevated temperature change is transmitted to reproductive cells so that the offsprings encode it in the genome, and it is better adapted to deal with elevated temperatures
question - How many species do this? Is it generally found throughout nature?
from - outube podcast interview - book - Understanding Living Systems - Ray Noble - Denis Noble - https://hyp.is/OUlGVBXrEe-iaBeZhH_4DQ/docdrop.org/video/oHZI1zZ_BhY/
-
-
-
organisms can actually go and use the chance and they're doing that all the time see the way our immune systems work shows that what happens when a new virus or new bacterium or new 00:02:56 anything else arrives
for - key insight - living systems use chance to adapt
key insight - living systems use chance to adapt - immune system defends against novel viruses - cancers grow - bacteria become resistant to antibiotics
-
-
-
four 00:08:25 major common misunderstandings that have infected our understanding of what it is to be a living system
for - molecular biology - paradigm shift - living system - 4 common misunderstandings - book - Understanding Living Systems - 4 common misunderstandings
4 common misunderstandings of living systems - 1. The central dogma of molecular biology - one way causation - Genes (DNA) to - proteins to - organism - 2. The Weismann Barrier - 3. DNA as self-replicator - 4. Separation of Replicator (DNA) and Vehicle (Living cell) are completely separate
-
biology Beyond The 00:00:19 genome
for - book - Biology Beyond the Genome - author - scientist - biologist - Denis Noble - book - Understanding Living Systems
-
- Apr 2024
-
-
Either system canbe s tart ed with a small li stof captions and be increasedscientifically.
Scientific principles had bled so thoroughly into both culture and business that even advertising for filing systems in business in the 1930 featured their ability to be used and expanded scientifically.
-
-
theconversation.com theconversation.com
-
And the evidence is coming back with unexpected results. A series of randomised controlled trials, including one looking at how to improve literacy through evidence, have suggested that schools that use methods based on research are not performing better than schools that do not.
This, too, is very logical. It is due to the nature of systems.
When one component, or even a lot, get "upgraded" this does not result in the overall results being improved. A system works best when all components work together to one or multiple goals in seemless harmony, creating emergence.
Therefore, if a component is out of place, even if it is better than its predecessor, it won't yield the correct results.
So for the methods to have a large, positive, impact, the entire system needs to be transformed.
This is why I don't want to upgrade a component of education at a time, but completely transform it once my theory of optimal education is complete. Like a phoenix, from the ashes we will rise. Burn it all down, and build it up again with an OODA loop at the core... The system needs to be in constant change, for without change, evolution cannot happen.
Observation Orientation Decision Action
This loop needs to be at the center of every system for "systems without the inherent capacity to change are doomed to die" -- Colonel John Boyd.
Of course, the system will need to be designed with utmost care and based on countless amounts of research, reviewed by a multitude of world-class experts in numeral areas.
-
-
Local file Local file
-
Stated briefly the work of the intelligence department can be 50brought under the three heads: filing, indexing and summarising.
For Kaiser, his "intelligence department" has three broad functions: summarizing, indexing, and filing.
Tags
Annotators
-
- Mar 2024
-
Local file Local file
-
It was said (76) that it isimpossible to devise a system wliich could be applied universally,the card registers give a very clear illustration of tliis.
This is a restatement that a particular system should be customized to its users.
There is potential that a system could be applied universally, but it requires a very large amount of data and metadata to suit the needs of a greater number of people and use cases. It also requires a reasonable amount of work in practical use to make it operate as expected.
The Mundaneum was likely close on paper and Google comes close to this, but still isn't perfect.
quote via ¶76 and 92
-
In each class the individual articles or the folders containing anumber of articles belonging to the same firm are numbered con-secutively, CI, C2, Tl, T2 etc. that is : a new series of consecutivenumbers is started with each initial letter. The correspondenceof Smith & Co. may for instance be in a folder marked C34, thecatalogues of Jones Bros, may be numbered T89. But theremay be a hundred letters to and from Smith & Co. and a dozencatalogues from Jones Bros, so that it will be necessary to dividefurther until each specific article will have a specific numberby which it can be quoted exclusively reserved to it. This isdone by suffixing the date to the previous numbers thus : C34-3VII7or T89-1906 etc. The former refers to a letter of Smith & Co.dated July the third 1907, the latter refers to a catalogue ofJones Bros, of 1906. No matter how large the files will becomein time, the meaning of these numbers will remain the same, andthere can be no other articles bearing these numbers. If a numberor numbers refer to more than one article, confusion is invariablythe result
Kaiser lays out an alphanumeric system for indexing materials using letters, numbers, and even dates and importantly suggests a 1-1 and onto relationship (though not in these terms) to prevent confusion.
Compare with Niklas Luhmann's system.
-
-
-
By 1700, we should note, slaves comprised half the population of thesouthern portion of the Carolina colony, an imbalance that widened to 72percent by 1740. Beginning in 1714, a series of laws required that for everysix slaves an owner purchased, he had to acquire one white servant.Lamenting that the “white population do not proportionally multiply,”South Carolina lawmakers had one more reason to wish that a corps ofLeet-men and women had actually been formed. Encouraged to marry andmultiply, tied to the land, they might have provided a racial and class barrierbetween the slaves and the landed elites.13
-
Slavery was thus a logicaloutgrowth of the colonial class system imagined by Hakluyt. It emergedfrom three interrelated phenomena: harsh labor conditions, the treatment ofindentures as commodities, and, most of all, the deliberate choice to breedchildren so that they should become an exploitable pool of workers.
-
-
Local file Local file
-
Katherine Sarafian,a producer who’s been at Pixar since Toy Story, tells me she prefers to envision triggering theprocess over trusting it—observing it to see where it’s faltering, then slapping it around a bitto make sure it’s awake. Again, the individual plays the active role, not the process itself. Or,to put it another way, it is up to the individual to remember that it’s okay to use the handle,just as long as you don’t forget the suitcase.
-
-
jods.mitpress.mit.edu jods.mitpress.mit.edu
-
-
By jumping into unfamiliar areas of code, even if you do not "solve" the bug, you can learn new areas of the code, tricks for getting up to speed quickly, and debugging techniques.
Building a mental model of the codebase, as Jennifer Moore says over at Jennifer++:
The fundamental task of software development is not writing out the syntax that will execute a program. The task is to build a mental model of that complex system, make sense of it, and manage it over time.
-
- Feb 2024
-
sr.ithaka.org sr.ithaka.org
-
to ensure a competitive marketplace for publishing through enterprise publishing systems
enterprise publishing systems:
-
-
www.biorxiv.org www.biorxiv.org
-
Transparent Peer Review
Download the complete Review Process [PDF] including:
- reviews
- authors' reply
- editorial decisions
-
-
ghs-garlandisdschools.libguides.com ghs-garlandisdschools.libguides.com
-
https://ghs-garlandisdschools.libguides.com/c.php?g=613369&p=7227110
Revisit this overview for extraction.
-
-
indubitablyodin.medium.com indubitablyodin.medium.com
-
Read [[Odin Halvorson]] in Indigenous Mnemonics and Personal Knowledge Management
I read in this area and this is the first I've heard the phrase IKS or “Indigenous Knowledge Systems”.
-
- Jan 2024
-
Local file Local file
-
Only reprints (without any alterations)retain the original call number, all revises or new editions howeversmall the alterations should be given a new call number, butdecimals may be used with advantage.
Though referring to catalogs and office literature, in 1908 it was known that using decimals would allow one to distinguish between slightly different versions of indexable items without running out of "space" for new additions.
-
Call Numbers
Interesting to see a mix of numbers and letters in the indexing system here from 1908.
Numbers for companies and dates and letters as tags for a variety of business purposes as well as for month indicators.
-
-
writingslowly.com writingslowly.com
-
I've sketched it out elsewhere but let's memorialize the broad strokes here because we're inspired at the moment... come back later and add in quotes from Luhmann and other sources (@Heyde1931).
Luhmann was balancing the differences between topically arranged commonplaces and the topical nature of the Dewey Decimal System (a standardized version across thousands of collections) and building neighborhoods of related ideas.
One of the issues with commonplace books, is planning them out in advance. How might you split up a notebook for long term use to create easy categories when you don't know how much room to give each in advance? (If you don't believe me, stop by r/commonplacebooks where you're likely to see this question pop up several times this year.) This issue is remedied when John Locke suggests keeping commonplaces in chronological order of their appearance and cross-indexing them.
This creates a new problem of a lot of indexing and increased searching over time as the commonplace book scales. Translating to index cards complicates things because they're unattached and can potentially move about, so they don't have the anchor effectuated by their being bound up in a notebook. But being on slips allows them to be more easily shuffled, rearranged, and even put into outlines, which are all fantastic affordances when looking for creativity or scaffolding things out into an article or book for creation.
As a result, numbering slips creates a solid anchor by which the cards can be placed and always returned for later finding and use. But how should we number them? Should it be with integers and done chronologically? (1, 2, 3, ..., n) This is nice, but makes a mish-mash of things and doesn't assist much in indexing or finding.
Why not go back to Dewey, which has been so popular? But not Dewey in the broadest sense of using numbers to tie ideas to concrete categories. An individual's notes are idiosyncratic and it would be increasingly rare for people to have the same note, much less need a standardized number for it (and if they were standardized, who does that work and how is it distributed so everyone could use it?) No, instead, let's just borrow the decimal structure of Dewey's system. One of the benefits of his decimal structure is that an infinity of new books can be placed on ever-expanding bookshelves without needing to restructure the numbering system. Just keep adding decimal places onto the end when necessary. This allows for immense density when necessary. But, importantly, it also provides some fantastic level of serendipity.
Let's say you go to learn about geometry, so you look up the topic in your trusty library card catalog. Do you really need to look at the hundreds of records returned? Probably not. You only need the the Dewey Decimal Number 516. Once you're at the shelves, you can browse through that section to see what's there and interesting in the space. You might also find things on the shelves above or below 516 and find the delights of topology and number theory or abstract algebra and real analysis. Subjects you might not necessarily have had in mind will suddenly present themselves for your consideration. Even if your initial interest may have been in Zhongmin Shen's Lectures on Finsler geometry (516.375), you might also profitably walk away with James E. Humphreys' Introduction to Lie Algebras and Representation Theory (512.55).
So what happens if we use these decimal numbers for our notes? First we will have the ability to file things between and amongst each other to infinity. By filing things closest to things which seem related to each other, we'll create neighborhoods of ideas which can easily grow over time. Related ideas will stay together while seemingly related ideas on first blush may slowly grow away from each other over time as even more closely related ideas move into the neighborhood between them. With time and careful work, you'll have not only a breadth of ideas, but a massive depth of them too.
The use of decimal numbering provides us with a few additional affordances:
1 (Neighborhoods of ideas) 1.1 combinatorial creativity Neighborhoods of ideas can help to fuel combinatorial creativity and forge new connections as well as insight over time. 1.2 writing One might take advantage of these growing neighborhoods to create new things. Perhaps you've been working for a while and you see you have a large number of cards in a particular area. You can, to some extent, put your hand into your box and grab a tranche of notes. By force of filing, these notes are going to be reasonably related, which means you should be able to use them to write a blog post, an article, a magazine piece, a chapter, or even an entire book (which may require a few fistfuls, as necessary.)
2 (Sparse indexing) We don't need to index each and every single topic or concept into our index. Because we've filed things nearby, if a new card about Finsler geometry relates to another and we've already indexed the first under that topic, then we don't need to index the second, because our future selves can easily rely on the fact that if we're interested in Finsler geometry in the future, we can look that up in the index, and go to that number where we're likely to see other cards related to the topic as well as additional serendipitous ideas related to them in that same neighborhood.
You may have heard that as Luhmann progressed on his decades long project, broadly on society and within the area of sociology, he managed to amass 90,000 index cards. How many do you suppose he indexed under the topic of sociology? Certainly he had 10s of thousands relating to his favorite subject, no? Of course he did, but what would happen over time as a collection grows? Having 20,000 indexed entries about sociology doesn't scale well for your search needs. Even 10 indexed entries may be a bit overwhelming as once you find a top level card, hundreds to thousands around it are going to be related. 10 x 100 = 1,000 cards to flip through. So if you're indexing, be conservative. In the roughly 45 years of creating 90,000 slips, Luhmann only indexed two cards with the topic of "sociology". If you look through his index, you'll find that most of his topical entries only have pointers to one or two cards, which provide an entryway into those topics which are backed up with dozens to hundreds of cards on related topics. In rarer, instances you might find three or four, but it's incredibly rare to find more than that.
Over time, one will find that, for the topics one is most interested in, the number of ideas and cards will grown without bound. Here it makes sense to use more and more specific topics (tags, categories, taxonomies) all of which are each also sparsely indexed. Ultimately one finds that in the limit, the categories get so fractionalized that the closest category one idea has with another is the fact that they're juxtaposed closely by number. The of the decimal expansion might say something about the depth or breadth of the relationship between ideas.
Something else arises here. At first one may have the tendency to associate their numbers with topical categories. This is only natural as it's a function at which humans all excel. But are those numbers really categories after a few weeks? Probably not. Treat them only as address numbers or GPS coordinates to be able to find your way. Your sociology section may quickly find itself with invasive species of ideas from anthropology and archaeology as well as history. If you treat all your ideas only at the topical level, they'll be miles away from where you need them to be as the smallest level atomic ideas collide with each other to generate new ideas for you. Naturally you can place them further away if you wish and attempt to bridge the distance with links to numbers in other locations, but I suspect you'll find this becomes pretty tedious over time and antithetical when it comes time to pull out a handful and write something. It's fantastically easier to pull out a several dozen and begin than it is to go through and need to pull out linked cards in a onesy-twosies manner or double check with your index to make sure you've gotten the most interesting bits. This becomes even more important as your collection scales.
-
-
Local file Local file
-
The physicistsStephen Wolfram and Brosl Hasslacher introduced me, in the early1980s, to chaos theory and nonlinear systems. In the 1990s, I learnedabout complex systems from conversations with Danny Hillis, the bi-ologist Stuart Kauffman, the Nobel-laureate physicist Murray Gell-Mann, and others. Most recently, Hasslacher and the electrical engineerand device physicist Mark Reed have been giving me insight into the in-credible possibilities of molecular electronics.
some of Bill Joy's intellectual history here mirrors much of my own...
-
-
www.derstandard.de www.derstandard.de
-
Der Standard informiert über zwei Studien, die unter anderem den Zusammenhang von Stadtentwicklung und globaler Erhitzung betreffen. Vor allem in den USA wird für die Mehrzahl der großen Städte eine Schrumpfung vorausgesagt, verstärkt durch die Folgen der Erhitzung. Die Studie verwendet ist Szenarien des IPCC. Unter anderem ergibt sich daraus die Forderung, die Stadtplanung nicht mehr vor allem an der Vorstellung von wachsenden Städten auszurichten. https://www.derstandard.de/story/3000000203501/tausende-us-staedte-koennten-bis-2100-zu-geisterorten-werden
-
-
-
Der Ausbau der Windenergie in Deutschland hat sich unter der Ampelkoalition beschleunigt. Es werden aber im Augenblick nur etwa halt so viele Anlagen gebaut, wie es nach den Plänen der Bundesregierung nötig wäre. In den südlichen Bundesländern ist der Ausbau viel zu langsam. Genehmigungsverfahren z.B. für den Transport dauern zu lange. https://taz.de/Ausbau-der-Windenergie/!5983011/
-
-
pileofindexcards.org pileofindexcards.org
-
You can order Correct’s indexcard, dock, and Kokuyo’s fieldnote via the Service page.
Hawk Sugano apparently offered the Pile of Index Cards as a physical product offering by combining Correct's index card dock and Kokuyo's fieldnotes in late December 2006.
-
-
web.archive.org web.archive.org
-
vielmetti.wordpress.com vielmetti.wordpress.com
-
Noguchi's book "Chou Seiri Hou (Ultra Management Technique)".
-
-
communicationnation.blogspot.com communicationnation.blogspot.com
-
de.wikipedia.org de.wikipedia.org
-
thetodaysystem.com thetodaysystem.com
-
I built the system out of necessity–because after trying my hand at the big names in personal productivity systems for years, I couldn’t quite get them to work for me. Out of that frustration, The Today System was born.
Mike Sturm ostensible created the Today System for his own use.
Is the system productized? Is he charging something for it or just proselytizing it?
-
- Dec 2023
-
docdrop.org docdrop.org
-
history is always the result of a lot of causes coming together you know 00:29:22 you have this metaphor of the chain of events and this is a terrible metaphor for there is no chain of events a chain of events imagines that every event is a link connected to one previous event and 00:29:36 to one subsequent event so there is a war there is one cause for the war and there will be one consequence it's never like that in history every event is more like a tree there is an entire system of 00:29:50 roots that came together to create it and it has a lot of fruits with lots of different influences
-
for: insight - history - complexity, bad metaphor - chain of events
-
insight: complexity and history
- chain of events is a bad metaphor for things that occur in history
- the complexity of history is that many causes come together too being about an event
- likewise, when that event occurs, it is the cause of many different consequences
- linear vs systems thinking
-
adjacency between
- history
- emptiness
- Indra's net
- adjacency statement
- history reflects emptiness
- Indra's net extended into historical events
-
-
what you're referring to is the idea that people come together and through language culture and story they have narratives that then create their own realities like the 00:12:04 sociologist abely the sociologist wi Thomas said if people think people believe things to be real then they are real in their consequences
-
for: Thomas Theorem, The definition of the situation, William Isaac Thomas, Dorothy Swain Thomas, definition - Thomas Theorem, definition - definition of the situation, conflicting belief systems - Thomas theorem, learned something new - Thomas theorem
-
definition: Thomas Theorem
- definition: definition of the situation
- "The Thomas theorem is a theory of sociology which was formulated in 1928 by William Isaac Thomas and Dorothy Swaine Thomas:
If men define situations as real, they are real in their consequences.[1]
In other words, the interpretation of a situation causes the action. This interpretation is not objective. Actions are affected by subjective perceptions of situations. Whether there even is an objectively correct interpretation is not important for the purposes of helping guide individuals' behavior.|
- comment
- learned something new
-
key insight: polarization
- Behaviors subsequently are enacted out of a set of beliefs.
- If there are a multitude of conflicting belief systems emerged from different cultures, then real conflicts can emerge out of the disharmony of conflicting beliefs
- This is a very important insight into the polarization we see in the world today
-
adjacency between:
- polarization
- Thomas Theorem
-
adjacency statement
- polarization can be explained by the Thomas Theorem
-
reference
-
Tags
- insight - history - complexity + emptiness
- adjacency - history - emptiness - Indra's net
- Adjacency - polarization - Thomas Theorem
- definition - Thomas Theorem
- key insight - Thomas Theorem
- conflicting belief systems - Thomas theorem
- definition - definition of the situation
- Yuval Noah Harari - linear vs systems thinking
- learned something new - Thomas theorem
Annotators
URL
-
-
archive.org archive.org
-
If I had a dollar for every organizational system I have tried, I could treat myself to a steak dinner in a fancy restaurant. (Hey! That’s not a bad ideal!) I’ve tried notebook organizers, card files, flip charts, a stop watch, and numerous labeling gadgets. I’ve tried refrigerator magnets, the buddy system, lots of books, and a bunch of classes and seminars. All of these were good tools and some of them had great ideas, but none of them worked for me. (p27)
-
I accomplished a couple of other things on that first day back into reality. First, with an evil Grinch-like smile | uprooted every household management system | had ever tried, and tore up every single 3x5 card in them. Then one by one, | roasted and toasted them in the fireplace until they were gone, gone, gone. Next, with equally fiendish delight, | speared my $35 namebrand notebook organizer with a marshmallow fork, and | roasted it too. It melted into oblivion, all but it’s ugly metal spine. Next, | prayed for my attitude and for help. And finally, | marched myself into Wal-mart and bought my first clear plastic bin, a two pound sack of M&M's, and a loaf of white bread. For better or worse, we have been pretty happy campers at my house ever since. (p6)
-
-
-
many people are complex systems thinkers even though they don't know it
-
for: example - systems thinking, quote -: many people are complex systems thinkers
-
quote:
- many people are complex systems thinkers even though they don't know it
- Thomas Homer-Dixon
-
date: 2023
-
examples: complex systems clichés
- the whole of greater than the sum of its parts
- nonlinearities
- the straw that broke the camels back
- emergence
- the whole of greater than the sum of its parts
-
comment
- the first one could be that systems are not the same as just all the parts
- the second one could also represent Tipping points and nonlinearities of complex systems
-
-
-
www.biorxiv.org www.biorxiv.org
-
Transparent Peer Review
Download the complete Review Process [PDF] including:
- reviews
- authors' reply
- editorial decisions
-
-
www.biorxiv.org www.biorxiv.org
-
Transparent Peer Review
Download the complete Review Process [PDF] including:
- reviews
- authors' reply
- editorial decisions
-
-
www.biorxiv.org www.biorxiv.org
-
Transparent Peer Review
Download the complete Review Process [PDF] including:
- reviews
- authors' reply
- editorial decisions
-
- Nov 2023
-
www.edge.org www.edge.orgEdge.org1
-
a viable system is one that can handle the variability of its environment. Or, as Ashby put it, only variety can absorb variety.
-
-
www.biorxiv.org www.biorxiv.org
-
Transparent Peer Review
Download the complete Review Process [PDF] including:
- reviews
- authors' reply
- editorial decisions
-
-
-
The nightmares of AI discrimination and exploitation are the lived reality of those I call the excoded
Defining 'excoded'
-
AI raises the stakes because now that data is not only used to make decisions about you, but rather to make deeply powerful inferences about people and communities. That data is training models that can be deployed, mobilized through automated systems that affect our fundamental rights and our access to whether you get a mortgage, a job interview, or even how much you’re paid. Thinking individually is only part of the equation now; you really need to think in terms of collective harm. Do I want to give up this data and have it be used to make decisions about people like me—a woman, a mother, a person with particular political beliefs?
Adding your data to AI models is a collective decision
-
-
theinformed.life theinformed.life
-
https://theinformed.life/
Hosted by Jorge Arango (https://jarango.com/)
-
-
everbookforever.com everbookforever.comEverbook1
-
Everbook appears to be a variation on some of the GTD, PKM, and productivity traditions done on larger loose slips of paper (instead of notebook style) with an incredibly lovely leather folder. There's a lot to like here for those stuck between love of slips and notebooks. Its reminiscent of project planning and to do methods using ring binders or FiloFaxes.
Tags
Annotators
URL
-
- Oct 2023
-
www.youtube.com www.youtube.com
-
https://www.youtube.com/watch?v=Dfk2KNXH6Go
Marketing video/unboxing-esque...
-
-
www.lrb.co.uk www.lrb.co.uk
-
‘convolution’ (as in, each of the folds of the brain)
overlap (ha!) with signals theory?
-
-
www.reddit.com www.reddit.com
-
Each page just has a page number at the top corner, as far as I can see. The German Wikipedia entry says that from notebook E, he numbered the front pages with Arabic numerals and the back pages with Roman numerals, so his notes began at both ends and met in the middle of the book. This is clear in the original, but hard to understand. And he would at least have been able to refer to his notes in the form {volume letter, page number}.It seems he didn’t number consecutive entries himself, but that in later Lichtenberg scholarship there developed an editorial convention to do so. After his death they only published his ‘aphorisms’, organised by theme, and later re-organised by date, but still missing his scientific and other writings.
-
-
Local file Local file
-
Zunächst war ich ein Jahr am Oberverwaltungsgericht Lüneburg zurOrganisation eines Referenz-Systems für Verwaltungsgerichtsent-scheidungen; das Gericht sollte sehen können, was an obergerichtli-chen Entscheidungen jeweils vorlag
In the early 1950s, Luhmann spent a year at the Lüneburg Higher Administrative Court organizing a reference system for the administrative court decisions to enable researchers to see what decisions had been made in the higher courts.
Though he had begun his zettelkasten during his studies, this referencing system may have influenced the structure of his own note taking system.
Can we pin the dates on these practices down more closely?
-
-
medium.com medium.com
-
when building on unenclosable P2P systems like Holochain, it’s actually possible to have it both ways: clean-energy projects that have the resources for large-scale impact and are not at risk of becoming corrupt in protection of proprietary business interests.
- for: competitive advantage, competitive advantage - unencloseable carriers in energy systems
- competitive advantage: unencloseable carriers
- when building on unenclosable P2P systems like Holochain,
- it’s actually possible to have it both ways:
- clean-energy projects that have the resources for large-scale impact and
- are not at risk of becoming corrupt in protection of proprietary business interests.
-
- Sep 2023
-
www.youtube.com www.youtube.com
-
08:00 his sword technique was adaptable, mendable, consistent with the complex nature of reality, that changes constantly, not resisting change but adapting self to it
- see zk on how a more dynamic approach to productivity and systems can help us reflect reality more closely, ever changing
Tags
Annotators
URL
-
-
-
Merchants and traders have a waste book (Sudelbuch, Klitterbuch in GermanI believe) in which they enter daily everything they purchase and sell,messily, without order. From this, it is transferred to their journal, whereeverything appears more systematic, and finally to a ledger, in double entryafter the Italian manner of bookkeeping, where one settles accounts witheach man, once as debtor and then as creditor. This deserves to be imitatedby scholars. First it should be entered in a book in which I record everythingas I see it or as it is given to me in my thoughts; then it may be enteredin another book in which the material is more separated and ordered, andthe ledger might then contain, in an ordered expression, the connectionsand explanations of the material that flow from it. [46]
—Georg Christoph Lichtenberg, Notebook E, #46, 1775–1776
In this single paragraph quote Lichtenberg, using the model of Italian bookkeepers of the 18th century, broadly outlines almost all of the note taking technique suggested by Sönke Ahrens in How to Take Smart Notes. He's got writing down and keeping fleeting notes as well as literature notes. (Keeping academic references would have been commonplace by this time.) He follows up with rewriting and expanding on the original note to create additional "explanations" and even "connections" (links) to create what Ahrens describes as permanent notes or which some would call evergreen notes.
Lichtenberg's version calls for the permanent notes to be "separated and ordered" and while he may have kept them in book format himself, it's easy to see from Konrad Gessner's suggestion at the use of slips centuries before, that one could easily put their permanent notes on index cards ("separated") and then number and index or categorize them ("ordered"). The only serious missing piece of Luhmann's version of a zettelkasten then are the ideas of placing related ideas nearby each other, though the idea of creating connections between notes is immediately adjacent to this, and his numbering system, which was broadly based on the popularity of Melvil Dewey's decimal system.
It may bear noticing that John Locke's indexing system for commonplace books was suggested, originally in French in 1685, and later in English in 1706. Given it's popularity, it's not unlikely that Lichtenberg would have been aware of it.
Given Lichtenberg's very popular waste books were known to have influenced Leo Tolstoy, Albert Einstein, Andre Breton, Friedrich Nietzsche, and Ludwig Wittgenstein. (Reference: Lichtenberg, Georg Christoph (2000). The Waste Books. New York: New York Review Books Classics. ISBN 978-0940322509.) It would not be hard to imagine that Niklas Luhmann would have also been aware of them.
Open questions: <br /> - did Lichtenberg number the entries in his own waste books? This would be early evidence toward the practice of numbering notes for future reference. Based on this text, it's obvious that the editor numbered the translated notes for this edition, were they Lichtenberg's numbering? - Is there evidence that Lichtenberg knew of Locke's indexing system? Did his waste books have an index?
Tags
- Niklas Luhmann's zettelkasten
- quotes
- Georg Christoph Lichtenberg
- John Locke
- Konrad Gessner
- zettelkasten numbering
- fleeting notes
- idea links
- academic writing
- note taking advice
- accounting influence on note taking
- numbering systems
- Sönke Ahrens
- zettelkasten transmission
- open questions
- Dewey Decimal System
- waste books
- intellectual history
Annotators
-
-
www.dropbox.com www.dropbox.com
-
MODAL JAZZ COMPOSlTlON G HARMONY
MODAL JAZZ COMPOSlTlON & HARMONY Miller, R 1996
-
-
theinformed.life theinformed.life
-
31:00 Zettelkasten as system for ongoing learning (not bound to an outcome)
- see zk on process vs outcomes
-
-
babel.hathitrust.org babel.hathitrust.org
-
https://babel.hathitrust.org/cgi/pt?id=mdp.39015071458213&seq=1
Modern Filing Systems<br /> Wagemaker Furniture Company, Ltd. 1904 furniture catalog
-
-
-
less well known is that the same person was really 00:01:02 interested in morphogenesis
- for: Alan Turing, morphogenesis, AI - morphogenesis, self-organizing systems
-
-
www.biorxiv.org www.biorxiv.org
-
Transparent Peer Review
Download the complete Review Process [PDF] including:
- reviews
- authors' reply
- editorial decisions
-


