- Aug 2023
-
docdrop.org docdrop.org
-
when we step into uncertainty, our bodies respond physiologically and mentally.
- for: transition, uncertainty, uncertainty - neuroscience, ingroup, outgroup, letting go, lifetime student
- paraphrase
- Uncertainty brings
- immune system deterioration
- brain cells wither and even die
- creativity and intelligence decrease
- We often go from fear to anger because fear is a state of certainty.
- We become morally judgmental, an extreme version of oneself.
- conservatives become ultra-conservative
- liberals become ultra liberal.
- because we retreat to a place of safety and familiarity.
- The problem is that the world changes.
- Since we have to adapt or die, if we want to shift from A to B,
- the first step is not B.
- the first step is to go from A to not A
- to let go of our biases and assumptions;
- to step into the very place that our brain evolved to avoid;
- to step into the place of the unknown.
- to step into a liminal space
- Uncertainty brings
- comment
- Uncertainty is uncomfortable
- and can drive us into our familiar, accepted, insular ingroup
- In other words, lead to greater social polarization.
- Adaptation requires us to step into the unknown.
- Big changes in our lives therefore require us to go
- from the familiar and comfortable space,
- to the unfamiliar and uncomfortable
- movement away from our comfort zone, as is happening as the polycrisis we face gains traction.
-
- Jul 2023
-
www.academia.edu www.academia.edu
-
“Biaya paling mahal hidup di Indonesia adalah biaya ketidakpastian (uncertainties),”
-
- May 2023
-
en.wikipedia.org en.wikipedia.org
-
The Hawthorne effect is a type of human behavior reactivity
explore relationships here with body doubling, observer effect (physics), and Heisenberg's uncertainty principle...
-
- Jan 2023
-
forum.zettelkasten.de forum.zettelkasten.de
-
Note 9/8j says - "There is a note in the Zettelkasten that contains the argument that refutes the claims on every other note. But this note disappears as soon as one opens the Zettelkasten. I.e. it appropriates a different number, changes position (or: disguises itself) and is then not to be found. A joker." Is he talking about some hypothetical note? What did he mean by disappearing? Can someone please shed some light on what he really meant?
On the Jokerzettel
9/8j Im Zettelkasten ist ein Zettel, der das Argument enthält, das die Behauptungen auf allen anderen Zetteln widerlegt.
Aber dieser Zettel verschwindet, sobald man den Zettelkasten aufzieht.
D.h. er nimmt eine andere Nummer an, verstellt sich und ist dann nicht zu finden.
Ein Joker.
—Niklas Luhmann, ZK II: Zettel 9/8j
Translation:
9/8j In the slip box is a slip containing the argument that refutes the claims on all the other slips. But this slip disappears as soon as you open the slip box. That is, he assumes a different number, disguises himself and then cannot be found. A joker.
Many have asked about the meaning of this jokerzettel over the past several years. Here's my slightly extended interpretation, based on my own practice with thousands of cards, about what Luhmann meant:
Imagine you've spent your life making and collecting notes and ideas and placing them lovingly on index cards. You've made tens of thousands and they're a major part of your daily workflow and support your life's work. They define you and how you think. You agree with Friedrich Nietzsche's concession to Heinrich Köselitz that “You are right — our writing tools take part in the forming of our thoughts.” Your time is alive with McLuhan's idea that "The medium is the message." or in which his friend John Culkin said, "We shape our tools and thereafter they shape us."
Eventually you're going to worry about accidentally throwing your cards away, people stealing or copying them, fires (oh! the fires), floods, or other natural disasters. You don't have the ability to do digital back ups yet. You ask yourself, can I truly trust my spouse not to destroy them?,What about accidents like dropping them all over the floor and needing to reorganize them or worse, the ghost in the machine should rear its head?
You'll fear the worst, but the worst only grows logarithmically in proportion to your collection.
Eventually you pass on opportunities elsewhere because you're worried about moving your ever-growing collection. What if the war should obliterate your work? Maybe you should take them into the war with you, because you can't bear to be apart?
If you grow up at a time when Schrodinger's cat is in the zeitgeist, you're definitely going to have nightmares that what's written on your cards could horrifyingly change every time you look at them. Worse, knowing about the Heisenberg Uncertainly Principle, you're deathly afraid that there might be cards, like electrons, which are always changing position in ways you'll never be able to know or predict.
As a systems theorist, you view your own note taking system as a input/output machine. Then you see Claude Shannon's "useless machine" (based on an idea of Marvin Minsky) whose only function is to switch itself off. You become horrified with the idea that the knowledge machine you've painstakingly built and have documented the ways it acts as an independent thought partner may somehow become self-aware and shut itself off!?!
https://www.youtube.com/watch?v=gNa9v8Z7Rac
And worst of all, on top of all this, all your hard work, effort, and untold hours of sweat creating thousands of cards will be wiped away by a potential unknowable single bit of information on a lone, malicious card and your only recourse is suicide, the unfortunate victim of dataism.
Of course, if you somehow manage to overcome the hurdle of suicidal thoughts, and your collection keeps growing without bound, then you're sure to die in a torrential whirlwind avalanche of information and cards, literally done in by information overload.
But, not wishing to admit any of this, much less all of this, you imagine a simple trickster, a joker, something silly. You write it down on yet another card and you file it away into the box, linked only to the card in front of it, the end of a short line of cards with nothing following it, because what could follow it? Put it out of your mind and hope your fears disappear away with it, lost in your box like the jokerzettel you imagined. You do this with a self-assured confidence that this way of making sense of the world works well for you, and you settle back into the methodical work of reading and writing, intent on making your next thousands of cards.
Tags
- Erwin Schrödinger
- useless machines
- fears
- ghost in the machine
- fear uncertainty and doubt
- death by zettelkasten
- note collection loss and damage
- Lila
- Niklas Luhmann
- dataism
- Schrödinger's cat
- Claude Shannon
- Ghostbusters
- Werner Heisenberg
- Niklas Luhmann's zettelkasten
- Heisenberg Uncertainty Principle
- jokerzettel
Annotators
URL
-
- Dec 2022
-
link.springer.com link.springer.com
-
We analyzed URLs cited in Twitter messages before and after the temporary interruption of the vaccine development on September 9, 2020 to investigate the presence of low credibility and malicious information. We show that the halt of the AstraZeneca clinical trials prompted tweets that cast doubt, fear and vaccine opposition. We discovered a strong presence of URLs from low credibility or malicious websites, as classified by independent fact-checking organizations or identified by web hosting infrastructure features. Moreover, we identified what appears to be coordinated operations to artificially promote some of these URLs hosted on malicious websites.
-
-
www.nature.com www.nature.com
-
We found that users who followed elites who made more false or inaccurate statements themselves shared news from lower-quality news outlets (as judged by both fact-checkers and politically-balanced crowds of laypeople), used more toxic language, and expressed more moral outrage.
Elite mis and disinformation sharers have a negative effect on followers.
-
In the co-share network, a cluster of websites shared more by conservatives is also shared more by users with higher misinformation exposure scores.
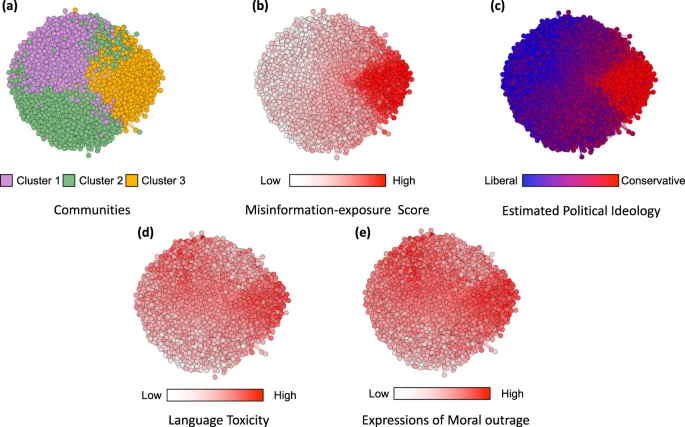
Nodes represent website domains shared by at least 20 users in our dataset and edges are weighted based on common users who shared them. a Separate colors represent different clusters of websites determined using community-detection algorithms29. b The intensity of the color of each node shows the average misinformation-exposure score of users who shared the website domain (darker = higher PolitiFact score). c Nodes’ color represents the average estimated ideology of the users who shared the website domain (red: conservative, blue: liberal). d The intensity of the color of each node shows the average use of language toxicity by users who shared the website domain (darker = higher use of toxic language). e The intensity of the color of each node shows the average expression of moral outrage by users who shared the website domain (darker = higher expression of moral outrage). Nodes are positioned using directed-force layout on the weighted network.
-
We found that misinformation-exposure scores are significantly positively related to language toxicity (Fig. 3a; b = 0.129, 95% CI = [0.098, 0.159], SE = 0.015, t (4121) = 8.323, p < 0.001; b = 0.319, 95% CI = [0.274, 0.365], SE = 0.023, t (4106) = 13.747, p < 0.001 when controlling for estimated ideology) and expressions of moral outrage (Fig. 3b; b = 0.107, 95% CI = [0.076, 0.137], SE = 0.015, t (4143) = 14.243, p < 0.001; b = 0.329, 95% CI = [0.283,0.374], SE = 0.023, t (4128) = 14.243, p < 0.001 when controlling for estimated ideology). See Supplementary Tables 1, 2 for full regression tables and Supplementary Tables 3–6 for the robustness of our results.
-
-
www.nature.com www.nature.com
-
The style is one that is now widely recognized as a tool of sowing doubt: the author just asked ‘reasonable’ questions, without making any evidence-based conclusions.Who is the audience of this story and who could potentially be targeted by such content? As Bratich argued, 9/11 represents a prototypical case of ‘national dissensus’ among American individuals, and an apparently legitimate case for raising concerns about the transparency of the US authorities13. It is indicative that whoever designed the launch of RT US knew how polarizing it would be to ask questions about the most painful part of the recent past.
-
-
www.nature.com www.nature.com
-
In the Irish sample, the combined vaccine hesitant and resistant group differed most pronouncedly from the vaccine acceptance group on the following psychological variables: lower levels of trust in scientists (d = 0.51), health care professionals (d = 0.45), and the state (d = 0.31); more negative attitudes toward migrants (d’s ranged from 0.27 to 0.29); lower cognitive reflection (d = 0.25); lower levels of altruism (d’s ranged from 0.17 to 0.24); higher levels of social dominance (d = 0.22) and authoritarianism (d = 0.14); higher levels of conspiratorial (d = 0.21) and religious (d = 0.20) beliefs; lower levels of the personality trait agreeableness (d = 0.15); and higher levels of internal locus of control (d = 0.14).
-
-
-
The only negative to this method is that it may not ALWAYS work. If the data is faulty, or the link is inaccurately provided by the sender, Gmail won’t be able to recognise and include the unsubscribe button in Gmail.
-
You may find this link isn’t available straight away, after a few emails one should appear, this is a common technique with mailing list providers.
-
-
zephoria.medium.com zephoria.medium.com
-
I often think back to MySpace’s downfall. In 2007, I penned a controversial blog post noting a division that was forming as teenagers self-segregated based on race and class in the US, splitting themselves between Facebook and MySpace. A few years later, I noted the role of the news media in this division, highlighting how media coverage about MySpace as scary, dangerous, and full of pedophiles (regardless of empirical evidence) helped make this division possible. The news media played a role in delegitimizing MySpace (aided and abetted by a team at Facebook, which was directly benefiting from this delegitimization work).
danah boyd argued in two separate pieces that teenagers self-segregated between MySpace and Facebook based on race and class and that the news media coverage of social media created fear, uncertainty, and doubt which fueled the split.
-
- Nov 2022
-
threadreaderapp.com threadreaderapp.com
-
Trope, trope, trope, strung into a Gish Gallop.
One of the issues we see in the Sunday morning news analysis shows (Meet the Press, Face the Nation, et al.) is that there is usually a large amount of context collapse mixed with lack of general knowledge about the topics at hand compounded with large doses of Gish Gallop and F.U.D. (fear, uncertainty, and doubt).
-
-
wexler.free.fr wexler.free.fr
-
Amos Tversky's famous "The Hot Hand in Basketball: On the Misperception of Random Sequences".
-
- Oct 2022
-
www.theatlantic.com www.theatlantic.com
-
Today, the people in politics who most often invoke the name of Jesus for their political causes tend to be the most merciless and judgmental, the most consumed by rage and fear and vengeance. They hate their enemies, and they seem to want to make more of them. They claim allegiance to the truth and yet they have embraced, even unwittingly, lies. They have inverted biblical ethics in the name of biblical ethics.
-
-
www.carproclub.com www.carproclub.com
-
Your Alternator Is Not A ChargerYes, you read that right. An alternator is designed to MAINTAIN your car battery, not recharge it from a deeply discharged state. Its designed to run at only 35-50% of its fully rated output. When you use your cars alternator to recharge a dead battery, you force it to run at nearly 100% of its rated capacity and that overheats the alternator and dramatically shortens its life.
This was the opinion also of https://hyp.is/YNQwwlF0Ee206UcS3HYLnA/www.reddit.com/r/Cartalk/comments/aoks7b/how_much_idling_needed_after_jump_start_to/
but are they misinformed?
-
-
github.com github.com
-
But this sounds like spreading fear and doubt when the Ruby parser has no such concepts :) {} always binds tightly to the call right next to it. This block {} will never go to using, unless it's rewritten as do ... end.
-
- Sep 2022
-
www.scientificamerican.com www.scientificamerican.com
-
We observed an overall increase in the amount of negative information as it passed along the chain—known as the social amplification of risk.
Could this be linked to my FUD thesis about decisions based on possibilities rather than realities?
-
-
developer.mozilla.org developer.mozilla.org
-
The request might or might not eventually be acted upon, as it might be disallowed when processing actually takes place.
-
- Aug 2022
-
www.theguardian.com www.theguardian.com
-
Sridhar, D. (2021, September 23). ‘I Know Who Caused Covid-19’ review – the global blame game. The Guardian. https://www.theguardian.com/books/2021/sep/23/i-know-who-caused-covid-19-review-the-global-blame-game
-
-
www.economist.com www.economist.com
-
The pandemic’s true death toll. (2021, November 1). The Economist. https://www.economist.com/graphic-detail/coronavirus-excess-deaths-estimates
-
-
www.sciencedirect.com www.sciencedirect.com
-
McKee, M., Altmann, D., Costello, A., Friston, K., Haque, Z., Khunti, K., Michie, S., Oni, T., Pagel, C., Pillay, D., Reicher, S., Salisbury, H., Scally, G., Yates, K., Bauld, L., Bear, L., Drury, J., Parker, M., Phoenix, A., … West, R. (2022). Open science communication: The first year of the UK’s Independent Scientific Advisory Group for Emergencies. Health Policy. https://doi.org/10.1016/j.healthpol.2022.01.006
-
-
www.bps.org.uk www.bps.org.uk
-
Decision-making in uncertainty | BPS. (n.d.). Retrieved November 22, 2021, from https://www.bps.org.uk/events/decision-making-uncertainty
-
-
gidmk.medium.com gidmk.medium.com
-
Nerd, G. M.-K. H. (2022, February 25). The Jury is Still Out on Ivermectin. Medium. https://gidmk.medium.com/the-jury-is-still-out-on-ivermectin-7d0a1895549
-
- Jul 2022
-
-
that's something that insect with a six-legged version is now it's the whole super organism oh well the ant colony is society that whole frame is actually the shadow of 01:18:52 what the evolutionary reality is which is that the ant colony is an organism not a super organism and the ants are tissues and so which level we prioritize or do we say no there's no a priori level ant is just i'm not even 01:19:05 gonna say there's anything out there called ants it's it's you how you're thinking about it or do we get lost or are we going to find a ladder in that multi-scale yeah well the latter is you know the 01:19:17 latter is active inference because it doesn't say active inference doesn't say make a make an internal model of the world that is accurate that actually accurately captures all the all the 01:19:30 details of the world of the universe that's not the point that's not what the mind does that's not the point the point is to act under uncertainty 01:19:41 given some useful model of the world act under uncertainty so that your fitness score improves and by fitness score here we essentially mean you know and anticipated uncertainty so i i would 01:19:55 very much like to be have some certainty that i'm going to be alive tomorrow and if it's freezing outside and i don't have a coat on uh you know that that becomes iffy so uh i'm going to be happy 01:20:06 if i'm going to be i'm going to go find a coat because it is going to reduce my uncertainty about survival over the next 24 hours but you can expand that you know outward right we we need to act the all organisms are acting under 01:20:19 uncertainty and and we can think about that as we can think about that um we can think from that perspective as a society of what are we doing and how do we measure 01:20:31 success well we're measuring success by acting under uncertainty and then re and then paying attention to what happens and then acting the same or differently or you know some other way or somehow some were 01:20:45 then choosing to act again in this cycle of act uh you know act uh process act process act process you know model act model act model that reminds me of course of the ooda 01:20:57 observe orient side act model and other sort of cyclic models of action and perception and then i would say that active inference provides a few nice little benefits over other phrasings of action and perception 01:21:10 qualitative and philosophical ones like inactivism as well as quantitative ones like cybernetics and other kinds of control theories so i totally agree this
An organism acts under uncertainty to reduce it to meet its objective.
Tags
Annotators
URL
-
- Jun 2022
-
Local file Local file
-
This fundamental tension—between quality and quantity—is atension we share as knowledge workers. We also must producework to an extremely high standard, and we must do it fast,continuously, all year long. We are like sprinters who are also tryingto run a marathon.
Do we? Really? This definitely needs reframing and books like this that play on these sorts of fears are both partially responsible, but are also preying on an atmosphere which they're propagating.
This is the sort of sad thing that a productivity guru would say...
-
-
globalecoguy.org globalecoguy.org
-
It’s as if we need the gravitational pull of both worlds to keep us on track, locked on a good and righteous path. Without both worlds pulling on us, we would crash into one, or simply lose our way, hurtling through the universe on our own, intersecting nothing, helping no one.
As neuroscietist Beau Lotto points out, the Anthropocene is creating greater and greater uncertainty and unpredictability, but the one human trait evolution has created to help us deal with this is the sense of awe. See my annotation on Beau Lotto's beautiful TED Talk: How we experience awe and why it matters https://hyp.is/go?url=http%3A%2F%2Fdocdrop.org%2Fvideo%2F17D5SrgBE6g%2F&group=world
In short, the sacred is the antidote to the increase in uncertainty and unpredictability as we enter into the space of the Anthropocene. Awe can be the leverage point to the ultimate leverage point for system change that Donella Meadows pointed out many years ago- it can lead to rapid shift in paradigms, worldviews and value systems needed to shift the system.
-
- Apr 2022
-
twitter.com twitter.com
-
Dr. Deepti Gurdasani [@dgurdasani1]. (2021, December 14). So those critiquing others for being too certain (I get subtweeted a lot for this)- Am I certain about the exact impact of omicron in the UK? Not at all Am I certain it’ll be high impact? Quite Am I certain we should act now? Absolutely [Tweet]. Twitter. https://twitter.com/dgurdasani1/status/1470828234480701443
-
-
twitter.com twitter.com
-
Julia Raifman. (2021, July 25). Policymakers are pointing fingers at “the unvaccinated” What if they gave them a hand instead? - Bring vax & food to workplaces, schools, homes -Fund local doctors, including pediatricians, to call patients & deliver vax—Learn from success of Indian Health Service approach [Tweet]. @JuliaRaifman. https://twitter.com/JuliaRaifman/status/1419288641885593604
-
- Feb 2022
-
www.cbsnews.com www.cbsnews.com
-
A cause of America’s labor shortage: Millions with long COVID. (n.d.). Retrieved February 2, 2022, from https://www.cbsnews.com/news/long-covid-labor-market-missing-workers/
-
- Jan 2022
-
en.wikipedia.org en.wikipedia.org
-
Goodhart's law is an adage often stated as "When a measure becomes a target, it ceases to be a good measure".[1] It is named after British economist Charles Goodhart, who advanced the idea in a 1975 article on monetary policy in the United Kingdom:[2][3] .mw-parser-output .templatequote{overflow:hidden;margin:1em 0;padding:0 40px}.mw-parser-output .templatequote .templatequotecite{line-height:1.5em;text-align:left;padding-left:1.6em;margin-top:0}Any observed statistical regularity will tend to collapse once pressure is placed upon it for control purposes.
We measure what we find important.
Measures can and often become self-fulfilling targets. (read: Rankings and Reactivity by W. Espeland and M. Sauder https://www.stmarys-ca.edu/sites/default/files/attachments/files/rankings-and-reactivity-2007.pdf)
When a measure becomes a target it ceases to be a good measure.
So why measure?
Is observation and measurement part of a larger complex process which isn't finished until the process itself is finished?
This seems related to the measurement problem in quantum mechanics, Schrödinger's cat, the Heisenberg uncertainty principle, and the observer effect).
-
- Dec 2021
-
-
Musicals, plays and pantos cancel shows after Covid-19 outbreaks. (2021, December 14). BBC News. https://www.bbc.com/news/entertainment-arts-59638954
-
-
twitter.com twitter.comTwitter1
-
Kristian G. Andersen on Twitter. (n.d.). Twitter. Retrieved 3 December 2021, from https://twitter.com/K_G_Andersen/status/1465822536629821442
-
- Nov 2021
-
www.theguardian.com www.theguardian.com
-
Wiseman, E. (2021, October 17). The dark side of wellness: The overlap between spiritual thinking and far-right conspiracies. The Observer. https://www.theguardian.com/lifeandstyle/2021/oct/17/eva-wiseman-conspirituality-the-dark-side-of-wellness-how-it-all-got-so-toxic
Tags
- wellness
- debunking
- science
- conspirituality
- is:news
- lang:en
- Center for Countering Digital Hate
- disinformation
- wellness industry
- online community
- conspiracy theory
- psychology
- right wing
- wellbeing
- health
- social media
- mental health
- spirituality
- influencer
- misinformation
- QAnon
- uncertainty
- anti-vaccine
- ideology
- worldview
- trust
- pseudoscience
- policy
- infodemic
Annotators
URL
-
-
-
Desforges, M., Gurdasani, D., Hamdy, A., & Leonardi, A. J. (2021). Uncertainty around the Long-Term Implications of COVID-19. Pathogens, 10(10), 1267. https://doi.org/10.3390/pathogens10101267
-
- Oct 2021
-
www.cambridge.org www.cambridge.org
-
Lagnado, D. A. (2022). Explaining the evidence: How the mind investigates the world. Cambridge University Press.
-
-
twitter.com twitter.com
-
Seth Trueger. (2021, September 14). Https://t.co/LFZ3xWkYYY [Tweet]. @MDaware. https://twitter.com/MDaware/status/1437780952890191878
-
-
-
Covid-19: ‘Vaccine misinformation a dilemma for young people’. (2021, September 19). BBC News. https://www.bbc.com/news/uk-northern-ireland-58616080
-
-
www.nature.com www.nature.com
-
Telenti, A., Arvin, A., Corey, L., Corti, D., Diamond, M. S., García-Sastre, A., Garry, R. F., Holmes, E. C., Pang, P., & Virgin, H. W. (2021). After the pandemic: perspectives on the future trajectory of COVID-19. Nature, 1–14. https://doi.org/10.1038/s41586-021-03792-w
-
- Sep 2021
-
-
Shu, J., Ochsner, K. N., & Phelps, E. A. (2021). The Impact of Intolerance of Uncertainty on Reappraisal and Suppression. PsyArXiv. https://doi.org/10.31234/osf.io/fsnvy
-
-
www.gavi.org www.gavi.org
-
Josh Michaud. “Over the next 2 Months COVAX Expects to Have Access to Almost Twice as Many Covid-19 Vaccine Doses as It Did over the First 8 Months of This Year. Https://Gavi.Org/Sites/Default/Files/Covid/Covax/COVAX-Supply-Forecast.Pdf Https://T.Co/JBtGYXFTwc.” Tweet. @joshmich (blog), September 2, 2021. https://twitter.com/joshmich/status/1433462474544660484.
-
- Aug 2021
-
royalsocietypublishing.org royalsocietypublishing.org
-
we find that fixing fossil ages to the midpoint or a random point drawn from within the stratigraphic age range leads to biases in divergence time estimates, while sampling fossil ages leads to estimates that are similar to inferences that employ the correct ages of fossils. Second, we show a comparison using an empirical dataset of extant and fossil cetaceans, which confirms that different methods of handling fossil age uncertainty lead to large differences in estimated node ages
dealing with uncertainties carefully actually matters
-
-
psyarxiv.com psyarxiv.com
-
Zarzeczna, N., Hanel, P. H. P., Rutjens, B., Bono, S. A., Chen, Y.-H., & Haddock, G. (2021). Scientists, speak up! Source impacts trust in and intentions to comply with health advice cross-culturally. PsyArXiv. https://doi.org/10.31234/osf.io/279yg
-
-
kerkour.com kerkour.com
-
Stop trying to connect all the dots ahead of time. Embrace uncertainty and start doing. “You can’t connect the dots looking forward; you can only connect them looking backwards. So you have to trust that the dots will somehow connect in your future. You have to trust in something — your gut, destiny, life, karma, whatever. This approach has never let me down, and it has made all the difference in my life." - Steve Jobs
decent write up, solid concluding quote.
-
-
blog.logrocket.com blog.logrocket.com
-
Before you go like “Wow!!!”, understand that the packages highlighted above take a lot into consideration when detecting timezones. This makes them slightly more accurate than Intl API alone.
What exactly does moment do for us, then, that
TimeFormat().resolvedOptions().timeZone;doesn't do? Name one example where it is more accurate.
-
-
www.cnn.com www.cnn.com
-
Covid-19: New poll shows why some vaccine-hesitant Americans decided to get the shot—CNNPolitics. (n.d.). Retrieved August 2, 2021, from https://edition.cnn.com/2021/07/13/politics/poll-covid-19-vaccine-decision/index.html
-
-
www.ncbi.nlm.nih.gov www.ncbi.nlm.nih.gov
-
Smith, M. J., Ahmad, A., Arawi, T., Dawson, A., Emanuel, E. J., Garani-Papadatos, T., Ghimire, P., Iliyasu, Z., Lei, R., Mastroleo, I., Mathur, R., Okeibunor, J., Parker, M., Saenz, C., Thomé, B., Upshur, R. E. G., & Voo, T. C. (2021). Top five ethical lessons of COVID-19 that the world must learn. Wellcome Open Research, 6, 17. https://doi.org/10.12688/wellcomeopenres.16568.1
-
- Jul 2021
-
-
Padilla, L., Hosseinpour, H., Fygenson, R., Howell, J., Chunara, R., & Bertini, E. (2021). Effects of COVID-19 Uncertainty Visualizations on Novice Risk Estimates. PsyArXiv. https://doi.org/10.31234/osf.io/6axc7
-
- Jun 2021
-
252f2edd-1c8b-49f5-9bb2-cb57bb47e4ba.filesusr.com 252f2edd-1c8b-49f5-9bb2-cb57bb47e4ba.filesusr.com
-
The Anti-Vaxx Playbook | Center for Countering Digital Hate. (n.d.). Retrieved June 26, 2021, from https://www.counterhate.com/playbook
-
- May 2021
-
80000hours.org 80000hours.org
-
Career decision making involves so much uncertainty that it’s easy to feel paralysed. Instead, make some hypotheses about which option is best, then identify key uncertainties: what information would most change your best guess?
We tend to think that uncertainties can't be weighted in our decision-making, but we bet on uncertainties all the time. Rather than throw your hands up and say, "I don't have enough information to make a call", how can we think deliberately about what information would reduce the uncertainty?
-
think of your career as a series of experiments designed to help you learn about yourself and test out potentially great longer-term paths
I wonder if there's a connection here to Duke, A. (2019). Thinking in Bets: Making Smarter Decisions When You Don’t Have All the Facts. Portfolio.
I haven't read the book but it's on my list.
-
-
www.theguardian.com www.theguardian.com
-
the Guardian. “How Good Are We at Predicting the Pandemic? | David Spiegelhalter & Anthony Masters,” May 9, 2021. http://www.theguardian.com/theobserver/commentisfree/2021/may/09/how-good-are-we-at-predicting-pandemic.
-
-
arxiv.org arxiv.org
-
Broniatowski, D. A., Kerchner, D., Farooq, F., Huang, X., Jamison, A. M., Dredze, M., & Quinn, S. C. (2020). The COVID-19 Social Media Infodemic Reflects Uncertainty and State-Sponsored Propaganda. ArXiv:2007.09682 [Physics]. http://arxiv.org/abs/2007.09682
-
- Mar 2021
-
twitter.com twitter.com
-
The BMJ on Twitter. (n.d.). Twitter. Retrieved 5 March 2021, from https://twitter.com/bmj_latest/status/1324962326127251457
-
- Feb 2021
-
www.scientificamerican.com www.scientificamerican.com
-
McKenna, S. (n.d.). COVID Models Show How to Avoid Future Lockdowns. Scientific American. Retrieved 26 February 2021, from https://www.scientificamerican.com/article/covid-models-show-how-to-avoid-future-lockdowns/
-
-
twitter.com twitter.com
-
ReconfigBehSci on Twitter: ‘RT @DrBrookeRogers: Universities and colleges face Covid funding shortfalls https://t.co/v2s0dVETBa’ / Twitter. (n.d.). Retrieved 24 February 2021, from https://twitter.com/SciBeh/status/1323575049425768448
-
-
www.bbc.co.uk www.bbc.co.uk
-
Universities and colleges face Covid funding shortfalls. (2020, November 3). BBC News. https://www.bbc.com/news/education-54780790
-
-
en.wikipedia.org en.wikipedia.org
-
In object-oriented programming, information hiding (by way of nesting of types) reduces software development risk by shifting the code's dependency on an uncertain implementation (design decision) onto a well-defined interface. Clients of the interface perform operations purely through it so if the implementation changes, the clients do not have to change.
-
- Dec 2020
-
www.nature.com www.nature.com
-
Ledford, H. (2020). Oxford COVID-vaccine paper highlights lingering unknowns about results. Nature. https://doi.org/10.1038/d41586-020-03504-w
-
- Oct 2020
-
stackoverflow.com stackoverflow.com
-
If you have a better/simpler/"more official" solution, I'd still love to see it!
The "official" solution is to use submitErrors (see Erik's answer).
-
-
en.wikipedia.org en.wikipedia.org
-
The Y-intercept of the SML is equal to the risk-free interest rate. The slope of the SML is equal to the market risk premium and reflects the risk return tradeoff at a given time: S M L : E ( R i ) = R f + β i [ E ( R M ) − R f ] {\displaystyle \mathrm {SML} :E(R_{i})=R_{f}+\beta _{i}[E(R_{M})-R_{f}]\,} where: E(Ri) is an expected return on security E(RM) is an expected return on market portfolio M β is a nondiversifiable or systematic risk RM is a market rate of return Rf is a risk-free rate
This is one statement of the key relationship.
The point is that the market will have a single tradeoff between unavoidable (nondiversifiable) risk and return.
Asset's returns must reflect this, according to the theory. Their prices will be bid up (or down), until this is the case ... the 'arbitrage' process.
Why? Because (assuming borrowing/lending at a risk free rate) *any investor can achieve a particular return for a given risk level simply by buying the 'diversified market basket' and leveraging this (for more risk) or investing the remainder in the risk free-asseet (for less risk). (And she can do no better than this.)
-
This abnormal extra return above the market's return at a given level of risk is what is called the alpha.
this is why you here the stock-touts bragging about their 'alpha'
-
-
en.wikipedia.org en.wikipedia.org
-
Capital asset pricing model
please read this article
-
quantity beta (β)
You hear about this 'beta' all the time as the measure of 'the correlation of the risk of an asset with the representative market basket'...
but confusingly, \(\beta\) is used to represent the slope of the expected return of an asset as this risk increases.
-
-
en.wikipedia.org en.wikipedia.org
-
If the fraction q {\displaystyle q} of a one-unit (e.g. one-million-dollar) portfolio is placed in asset X and the fraction 1 − q {\displaystyle 1-q} is placed in Y, the stochastic portfolio return is q x + ( 1 − q ) y {\displaystyle qx+(1-q)y} . If x {\displaystyle x} and y {\displaystyle y} are uncorrelated, the variance of portfolio return is var ( q x + ( 1 − q ) y ) = q 2 σ x 2 + ( 1 − q ) 2 σ y 2 {\displaystyle {\text{var}}(qx+(1-q)y)=q^{2}\sigma _{x}^{2}+(1-q)^{2}\sigma _{y}^{2}} . The variance-minimizing value of q {\displaystyle q} is q = σ y 2 / [ σ x 2 + σ y 2 ] {\displaystyle q=\sigma _{y}^{2}/[\sigma _{x}^{2}+\sigma _{y}^{2}]} , which is strictly between 0 {\displaystyle 0} and 1 {\displaystyle 1} . Using this value of q {\displaystyle q} in the expression for the variance of portfolio return gives the latter as σ x 2 σ y 2 / [ σ x 2 + σ y 2 ] {\displaystyle \sigma _{x}^{2}\sigma _{y}^{2}/[\sigma _{x}^{2}+\sigma _{y}^{2}]} , which is less than what it would be at either of the undiversified values q = 1 {\displaystyle q=1} and q = 0 {\displaystyle q=0} (which respectively give portfolio return variance of σ x 2 {\displaystyle \sigma _{x}^{2}} and σ y 2 {\displaystyle \sigma _{y}^{2}} ). Note that the favorable effect of diversification on portfolio variance would be enhanced if x {\displaystyle x} and y {\displaystyle y} were negatively correlated but diminished (though not eliminated) if they were positively correlated.
Key building block formulae.
Start with 'what happens to the variance when we combine two assets (uncorrelated with same expected return)'
What are the variance minimizing shares and what is the resulting variance of the portfolio.
-
Similarly, a 1985 book reported that most value from diversification comes from the first 15 or 20 different stocks in a portfolio.[6]
the conventional wisdom is that there are sharply diminishing returns to this diversification
-
-
www.bmj.com www.bmj.com
-
Smith, G. D., Blastland, M., & Munafò, M. (2020). Covid-19’s known unknowns. BMJ, 371. https://doi.org/10.1136/bmj.m3979
-
-
www.thelancet.com www.thelancet.com
-
Brown, R. C. H., Kelly, D., Wilkinson, D., & Savulescu, J. (2020). The scientific and ethical feasibility of immunity passports. The Lancet Infectious Diseases, 0(0). https://doi.org/10.1016/S1473-3099(20)30766-0
-
-
www.agileconnection.com www.agileconnection.com
-
This balancing act needs to take into account project complexity (size, distribution, etc.), uncertainty (risk, innovation need, etc.), and the cost of change at the project level and for each major component.
-
-
dylanvann.com dylanvann.com
-
Disclaimer: I’m new to Svelte so this isn’t so much a recommendation as it is a “I guess this is a way to do it 🤷♂️”
-
-
covid-19.iza.org covid-19.iza.org
-
COVID-19 and the Labor Market. (n.d.). IZA – Institute of Labor Economics. Retrieved October 11, 2020, from https://covid-19.iza.org/publications/dp13632/
-
-
covid-19.iza.org covid-19.iza.org
-
COVID-19 and the Labor Market. (n.d.). IZA – Institute of Labor Economics. Retrieved October 10, 2020, from https://covid-19.iza.org/publications/dp13569/
-
-
www.pewresearch.org www.pewresearch.org
-
NW, 1615 L. St, Suite 800Washington, & Inquiries, D. 20036USA202-419-4300 | M.-857-8562 | F.-419-4372 | M. (2020, September 17). U.S. Public Now Divided Over Whether To Get COVID-19 Vaccine. Pew Research Center Science & Society. https://www.pewresearch.org/science/2020/09/17/u-s-public-now-divided-over-whether-to-get-covid-19-vaccine/
-
- Sep 2020
-
www.theatlantic.com www.theatlantic.com
-
The challenge is to find a way to live with uncertainty,
Finding a way to be okay with uncertainty in life is a challenge for many people. I struggle with this as well. But over the last few months I have found various ways to cope with the anxiety caused by uncertainty. Because the world we live in today is full of uncertainties.
-
-
psyarxiv.com psyarxiv.com
-
Haas, I. J., Baker, M., & Gonzalez, F. (2020). Political Uncertainty Moderates Neural Evaluation of Incongruent Policy Positions. https://doi.org/10.31234/osf.io/bmr59
-
-
www.scotsman.com www.scotsman.com
-
Beware comforting lies about a “herd immunity” Covid-19 strategy. Here’s why it’s dangerous – Professor Devi Sridhar. (n.d.). Retrieved September 25, 2020, from https://www.scotsman.com/news/opinion/columnists/covid-19-herd-immunity-strategy-flawed-until-we-have-coronavirus-vaccine-professor-devi-sridhar-2981017
Tags
- antibody
- vaccine
- epidemiology
- strategy
- is:news
- protection
- herd immunity
- lang:en
- government response
- prediction
- uncertainty
- COVID-19
- safety
Annotators
URL
-
-
www.thelancet.com www.thelancet.com
-
Houlihan, C. F., & Beale, R. (2020). The complexities of SARS-CoV-2 serology. The Lancet Infectious Diseases, 0(0). https://doi.org/10.1016/S1473-3099(20)30699-X
-
-
osf.io osf.io
-
Hennessy, E. A., Acabchuk, R., Arnold, P. A., Dunn, A. G., Foo, Y. Z., Johnson, B. T., Geange, S. R., Haddaway, N. R., Nakagawa, S., Mapanga, W., Mengersen, K., Page, M. J., Sánchez-Tójar, A., Welch, V., & McGuinness, L. A. (2020). Ensuring Prevention Science Research is Synthesis-Ready for Immediate and Lasting Scientific Impact [Preprint]. MetaArXiv. https://doi.org/10.31222/osf.io/ptg9j
-
-
ncrc.jhsph.edu ncrc.jhsph.edu
-
The Contagion Externality of a Superspreading Event: The Sturgis Motorcycle Rally and COVID-19 | NCRC. (2020, September 3). 2019 Novel Coronavirus Research Compendium (NCRC). https://ncrc.jhsph.edu/research/the-contagion-externality-of-a-superspreading-event-the-sturgis-motorcycle-rally-and-covid-19/
-
-
-
Thomas, D., & Giles, C. (2020, September 14). Cities count cost of lasting exodus from offices. https://www.ft.com/content/203cc83c-72b0-49c9-bea5-6fb38735a8fc
-
-
twitter.com twitter.com
-
(((Howard Forman))) on Twitter. (n.d.). Twitter. Retrieved September 16, 2020, from https://twitter.com/thehowie/status/1305232493071736834
-
-
www.bmj.com www.bmj.com
-
Siemieniuk, R. A., Bartoszko, J. J., Ge, L., Zeraatkar, D., Izcovich, A., Kum, E., Pardo-Hernandez, H., Rochwerg, B., Lamontagne, F., Han, M. A., Liu, Q., Agarwal, A., Agoritsas, T., Chu, D. K., Couban, R., Darzi, A., Devji, T., Fang, B., Fang, C., … Brignardello-Petersen, R. (2020). Drug treatments for covid-19: Living systematic review and network meta-analysis. BMJ, 370. https://doi.org/10.1136/bmj.m2980
-
-
www.reuters.com www.reuters.com
-
Exclusive: In Russia, a black market for HIV drug to try on coronavirus. (2020, April 20). Reuters. https://www.reuters.com/article/us-health-coronavirus-russia-hiv-exclusi-idUSKBN2220W1
-
-
-
Postdocs in crisis: Science cannot risk losing the next generation. (2020). Nature, 585(7824), 160–160. https://doi.org/10.1038/d41586-020-02541-9
-
-
www.thelancet.com www.thelancet.com
-
Chatterjee, Patralekha. ‘Is India Missing COVID-19 Deaths?’ The Lancet 396, no. 10252 (5 September 2020): 657. https://doi.org/10.1016/S0140-6736(20)31857-2.
-
-
www.hsph.harvard.edu www.hsph.harvard.edu
-
Boston, 677 Huntington Avenue, & Ma 02115 +1495‑1000. (2020, March 4). Coronavirus (COVID-19): Press Conference with Marc Lipsitch, 03/04/20. News. https://www.hsph.harvard.edu/news/features/coronavirus-covid-19-press-conference-with-marc-lipsitch-03-04-20/
-
-
www.thelancet.com www.thelancet.com
-
Yelin, D., Wirtheim, E., Vetter, P., Kalil, A. C., Bruchfeld, J., Runold, M., Guaraldi, G., Mussini, C., Gudiol, C., Pujol, M., Bandera, A., Scudeller, L., Paul, M., Kaiser, L., & Leibovici, L. (2020). Long-term consequences of COVID-19: Research needs. The Lancet Infectious Diseases, 0(0). https://doi.org/10.1016/S1473-3099(20)30701-5
-
- Aug 2020
-
annehelen.substack.com annehelen.substack.com
-
Petersen, A. H. (n.d.). Between f**ked and a hard place. Retrieved August 30, 2020, from https://annehelen.substack.com/p/between-fked-and-a-hard-place
-
-
hscif.org hscif.org
-
Humanities & Social Change (2020, April 30). Cultures of expertise and politics of behavioral science: A conversation with Erik Angner. https://hscif.org/cultures-of-expertise-and-politics-of-behavioral-science-a-conversation-with-erik-angner/
-
-
-
Hoffman, J. (2020, August 16). Fearing a ‘Twindemic,’ Health Experts Push Urgently for Flu Shots. The New York Times. https://www.nytimes.com/2020/08/16/health/coronavirus-flu-vaccine-twindemic.html
-
-
-
Baker, S. R., Bloom, N., & Terry, S. J. (2020). Using Disasters to Estimate the Impact of Uncertainty (Working Paper No. 27167; Working Paper Series). National Bureau of Economic Research. https://doi.org/10.3386/w27167
-
-
elemental.medium.com elemental.medium.com
-
ScD, N. N. A. (2020, June 11). A Guide to Understanding Pandemic Predictions. Medium. https://elemental.medium.com/a-guide-to-understanding-pandemic-predictions-8ae3439b8224
-
-
csbs.research.illinois.edu csbs.research.illinois.edu
-
Understanding Contemporary Challenges – Center for Social & Behavioral Science. (n.d.). Retrieved August 26, 2020, from https://csbs.research.illinois.edu/understandingcontemporarychallenges/
-
-
www.indiebound.org www.indiebound.org
-
The Lady’s Handbook for Her Mysterious Illness: A Memoir | IndieBound.org. (n.d.). Retrieved August 26, 2020, from https://www.indiebound.org/book/9780385534079
-
-
psyarxiv.com psyarxiv.com
-
Fife, D., Lung, M., Sullivan, N., & Young, C. (2020). When Values Collide: Why Scientists Argue About Open Science and How to Move Forward [Preprint]. PsyArXiv. https://doi.org/10.31234/osf.io/q9d28
-
-
riskytalk.libsyn.com riskytalk.libsyn.com
-
Risky Talk: Communicating Evidence in a Pandemic. (n.d.). Retrieved August 24, 2020, from https://riskytalk.libsyn.com/communicating-evidence-in-a-pandemic
-
-
www.forbes.com www.forbes.com
-
Togoh, I. (n.d.). After Hydroxychloroquine, Trump Is Now Seeking To Get Another Unproven Drug Approved By The FDA: Report. Forbes. Retrieved August 22, 2020, from https://www.forbes.com/sites/isabeltogoh/2020/08/17/after-hydroxychloroquine-trump-is-now-seeking-to-get-another-unproven-drug-approved-by-the-fda-report/
-